Stone Boiling

Indians of the early Southwest used the technique "stone boiling" to cook tender parts of bison, particularly the liver. Upon a successful hunt the paunch and liver were cut from a bison. Fire wood was gathered, stacked in criss-crossed layers, topped with stones then set afire. Nearby, the paunch was inverted, filled with water and hung upon a tripod of branches.

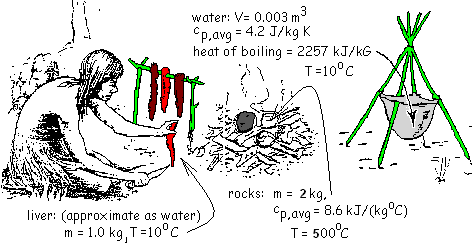As one Indian sliced liver, others replenished the fire until the stones were very hot. Finally using sticks the "cook" lifted the hot stones from the fire and dropped them, along with sliced liver, into the bag of water. A sketch of the event with the initial conditions of the stones, liver and water, is shown.
Determine the second temperature of the rock, water and liver in the bag.

♦ We take the rock, water and liver (approximated as an equal mass of water) as system. Ignore the thermal effects of the paunch. A precise second temperature cannot be determined because there will be heat to the cold atmospheric surroundings. The best we can do at this level is to approximate the event as adiabatic and calculate the greatest possible second temperature of the liver and water. There will be negligible kinetic and potential energy changes. The energy equation and its reduction for this event is:

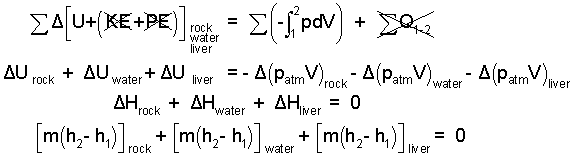
(1) 1

The rock is initially 500°C and the water and liver 10°C. Once together, a second, uniform temperature will be attained. There is no heat for this event because (i) we assume heat to the surrounding air as zero and (ii) we defined both the rock, water and liver as system. Such thermal aspect here is not heat but "thermal equilibration".

We anticipate the final temperature to be in the range: 10°C < T₂ < 500°C. The rock will remain solid. We don't know if the water will boil. To proceed, we assume the final phase of water is liquid and that the water and liver have the same properties - so we combine them.

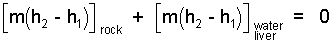(2)2

We will use "average specific heats" to solve. The first step is to construct the enthalpy differences. Since we have assumed no phase change the enthalpies of the second states will equal those of the initial state plus a change. These are written as follows:

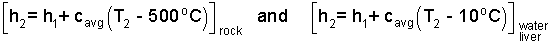
(3)3

Enter these enthalpies into the energy equation. Notice the initial enthalpies sum to zero.

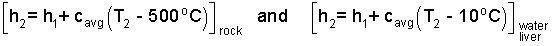
(4) 4

While we develop this equation we keep all terms "left of equality." There is no heat. There is work. It is the work of expansion of water against the atmosphere. These works were combined with the internal energy changes making them enthalpy changes. Take the above equation a step further, the initial enthalpies sum to zero leaving only the energy changes - stone relative to water (as written below).

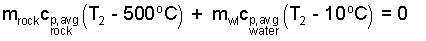
(5) 5

The second temperature will surely be less than 500°C. The first term, the energy change of the rock, is negative, as it should be - the energy of the rock decreases. Also the "water plus liver" term is positive. We can put numbers in this now.

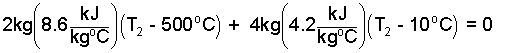
(6)6

From this we determine the second temperature to be, T₂ = 258°C! But this is impossible since it is well above 100^oC, the boiling temperature of water at 1 atmosphere. We conclude our assumption that the water remained liquid was wrong.

Assume the final phase of water is liquid and vapor.

To be careful, we will treat the water and liver separately. We write a mass equation for the water which expresses that liquid and gas exist in the final state.

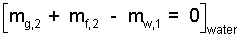
(7)7

Next we "postulate" the energy changes.

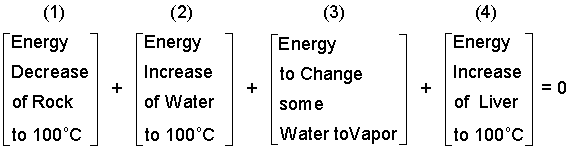
(8)8

By our assumption of liquid and vapor water in the second state, the second temperature will be 100°C which we use in the next equation. We have kept the terms in position. Next we enter data for specific heats and the enthalpy boiling, h_fg

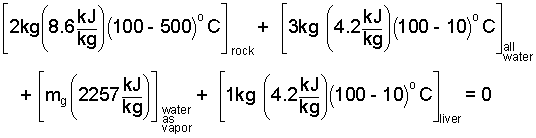
(9) 9

The only unknown quantity becomes the mass of the water (m_g) that is vapor upon conclusion of the assumed adiabatic event.

By careful calculation, the equation yields the amount of gas (or vapor) created to be,
m_g = 2.4kg. Consequently the second temperature is T₂ = 100°C.