18 Wheeler Safe-Braking Speeds

The "braking event" of an 18-Wheeler falls in the category "energy is conserved " (at least temporarily). When the fast-moving truck brakes, its kinetic energy transforms into increased internal energy of the truck. This energy resides (for the event) principally in the brake shoes and drums. By basic physics we know increased internal energy of a solid is exhibited by its increase of temperature (with the material mass and the specific heat as factors of proportion). In this example, we stop a big truck safely so the brakes get hot but are not ruined.

Tractor-trailer trucks are driven cautiously to avoid severe braking which can destroy brake drums.

Should a braking event (or an event of repeated braking) cause the temperature of a brake drum to exceed 800°F, either immediate failure to stop or permanent distortion of the brake drum might occur. Consider a fully-loaded rig with total mass of 80,000 pounds traveling on a flat, straight and level road. The 18 brake drums equals of the truck are steel. The combined mass, brake shoes and drums, is 120 pounds.

Calculate the maximum road speed for an emergency stop without brake damage.
♦ We model the truck as an extended body, of which the steel brakes are an interior part. The event is "increment" in form. It commences when the driver slams on the brakes and ends when the truck has stopped completely.

To just barge ahead, we adjust our extended body energy equation. Since the brakes will get smoking hot, we add internal energy. And given time, the brakes will cool. That effect would involve heat. Our "adjusted" energy equation for this system and its event is:

(1) 1

Over the short time of an emergency stop, friction (work) within the brakes will cause them to become quite hot. This is an increase of internal energy of the brakes. For the brakes to cool, for there to be enough heat for their temperature to abate, requires time. We model the stop as occurring to fast for there to be heat, thus we assume ΣQ_1-2 = 0. More will be said about heat later.

With work, stopping forces will occur where the tires meet the road, but assuming the truck does not slide, those forces are not displaced and there is no work. Seen in another way, the tires do not tear up the road - hence no work. Also, with this first calculation we assume the truck is traveling with the wind so there is no wind drag and no work associated with wind forces. Hence, in our equation, for the event, both work and heat are zero.

(2) 2

Summation signs are used to remind us that systems that have parts. We expand the equation to address the parts: the brakes and the rest of the truck.

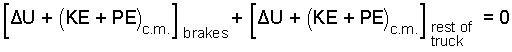(3) 3

In stopping on a flat road, neither the truck nor brakes experience change of potential energy. When the brakes get hot, their internal energy increases but the internal energy of the rest of the truck remains what it was.

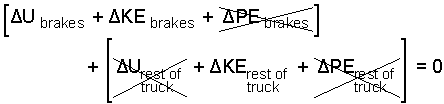(4) 4

The brakes and the rest of the truck have the same change of kinetic energy.

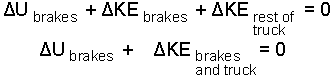(5) 5

Our equation makes sense. The kinetic energy of the entire truck (brakes included) decreases. By design of the braking system, none of that energy passes to the surroundings (bad design?). To stop, the entire kinetic energy is relocated into the drums (and shoes) which become smoking hot (increased internal energy is evidenced the new, high temperature).

From physics, change of internal energy equals mass times specific heat times temperature difference and change of kinetic energy equals one half the mass times the difference, of (speed - squared).

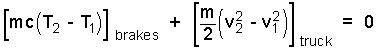(6)6

The specific heat of iron is 0.1 Btu / lbm °F. A reasonable number for the initial temperature of the brakes is 100°F. The brakes are slammed at time "1" and at "2" the truck has stopped. Rewrite and focus the equation:

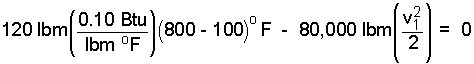(7) 7

The unit conversions, "Btu = 778 ft lbf " and "1 = 32.2 (lbm ft / lbf s²)" are required.

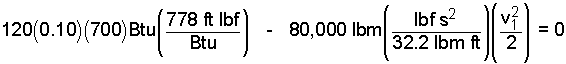(8) 8

Thus we determine the maximum safe speed as:

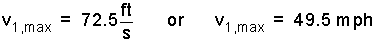(9) 9

To model the truck as an extended body is reasonable for accelerating or driving straight (on a perfect roadway. For braking however, the model is valid only when all of the brakes (those on the steering axle, the tractor axle and trailer axle) work in "precise unison" on an ideal roadway.

In real emergency stops, invariably the brakes of one axle attempt to do "all of the stopping". The "brakes" of one axle lock and skid. If steering axle brakes lock, the driver cannot steer and the truck goes straight. If tractor brakes lock the truck will jack-knife. For trailer brake to to lock is good at low speed. But if the rig is moving at a good clip and to stop, the trailer brakes lock, the rig will likely fish-tail into a nearby ditch. Only for the first-type event does the model of a truck as an "extended body" make sense.