Atwood's Machine

The surface acceleration of falling objecte was widely studied during and after Newton's Many attempts using many devices were used. The task was difficult since the natural fall of an object occurs with relatively great changes of height in quite short spans of time. A clever scheme was needed to quantify gravity.

Some forty years after Newton, the Reverend George Atwood devised and built an ingeneous apparatus to measure surface magnitude of acceleration. So successful was his method and device, that all devices developed thereafter to measure Earth's acceleration of gravity were called "Atwood Machines."

Atwood's method was to "slow" the "free fall" so its acceleration could be measured. To describe his apparatus and how it functioned requires careful writing (and reading). Each test of Atwood's machine of Earth's gravity has three stages: Setup, Free Fall and Final Velocity determination.

Setup: The apparatus consists of two equal masses connected one to the other by a long, thin cord that passes over a heated metal cylinder. When one mass moves so must the other and the cord is waxed such that it can slide over the cylinder with (almost) no friction.

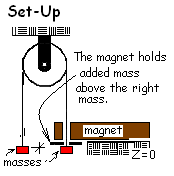
In balance, the masses support each other and are adjusted to have equal elevations. That elevation we set as a reference, ~ Z = 0. Slightly above the mass on the right, an electro-magnet holds a small iron, annular disc call an "added mass" (notated δm). Precise amounts for the two identical masses and for the added mass were previously selected. A final task of the setup is to select a distance through which the right mass and the added mass will accelerate together; L₁ (see figure: Stage I).

Each test to determine Earth's gravity consists of two stages; see figures, Stage I and Stage II.

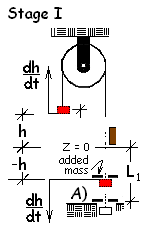
Stage I: When the magnet is shut off the added mass (δm) is released to drop lightly onto the right mass. Motion commences with all masses at elevation Z = 0, with zero velocity, under the motive of the "effective" gravity force ( a fraction of g_o,Earth) that the masses experience. Both right side masses descend, accelerate downward. The speeds of the left mass and the right masses are always equal. Stage I shows the apparatus in an intermediate position of the first, accelerating part of the test.

A relation for the "effective" downward acceleration (g_eff) in terms of the Earth surface value (g_o,Earth) can be obtained from the Rate form of the energy equation applied to the system.

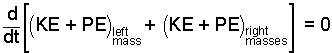(1) The system is the three masses and Earth.
Recall that the gravity force-displacement effect
has been represented as potential energy.

The kinetic and potential energies of the masses are promptly expressed in terms of their elevations and speeds.

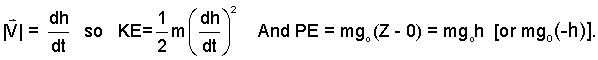(2)All masses have the same speed. The PE
of the right-side masses diminishes.

Whenever the construct, potential energy, is used, the system includes Earth. That point is often not stressed. Next express the energies in terms of speeds and elevations.

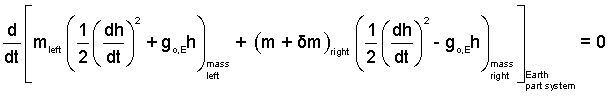
(3) For the event, there is no velocity or elevation
change of Earth. Thus Earth is part of the system
but it does nothing."

Practically every time we've seen an equation like this we've separated the variables. It is a little trick not to do that here. Let the differential operator act on the terms within the brackets.

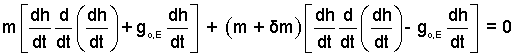(4)

The term below left is the derivative of a derivative. Such terms are also called "second" derivatives and can be written as below right. These forms are equivalent; we will use the left representation.

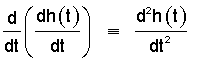(5) Equivalent expressions of the
second derivative.

Algbra applied to (4) yields this result:

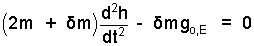(6) ♦

This solution seeks an algebraic result. Consequently we are doing algebra.

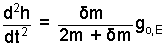
(7) 7

STAGE II: The figure shows the ingenious way Atwood "removed" the added mass.

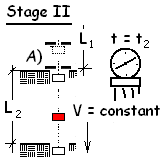
As the right side mass and added mass accelerated downward, at the distance L₁, they encountered an opening large enough for the mass to pass through but too small for the added mass to continue. At the instant the added mass is removed, acceleration ceases. After that instant both the left and right masses reverted to constant velocity motion each with the velocity, V*. The masses, added mass, L₁ and L₂ can be selected so that V* is slow enough to permit easy measurement of the time expended as it moves to the second level L₂.

Now return to equation (7). We write with three conditions: the initial speed, final speed.

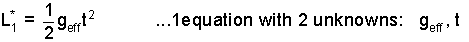(8) 8

The terminal speed V*₁ is measured in Stage II.

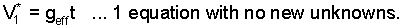(9) 9

The two equations above are solved for g_eff, the effective acceleration of the Atwood Machine. The masses, m and the added mass δm are known. The next equation is solved for g_o,Earth.

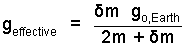(10) 10

The value obtained is about 9.81 m/s². Many texts use the number 9.8067. It is a very, very expensive Atwood's Machine that can decide the number is not 9.8068 and not 9.8066, but 9.8067. To carry more than two places of accuracy with these and others numbers costs time, yields nothing.