Car Drives Uphill

A car that weighs 3000 N has been tested thoroughly. Under full power its engine produces 160 kW of power (in excess of internal losses, rolling friction and other losses). Traveling top speed on a level road it attains a maximum speed is 35 m/s. Suppose the car were to travel up a hill with a rise of 1 meter for every 20 meters traveled. What constant speed would be expected?

We take the car as our system. Since the car will have internal friction and an operating temperature, we model it not as a BODY but as a simple compressible substance. The energy equation is:

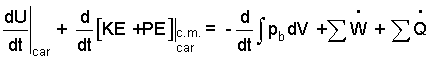
(1)The car is modeled as a "simple compressible substance.

First we consider the case of horizontal motion; the energy equation reduces as follows:

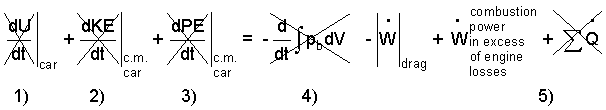
(2)Work is expanded to represent its power
and drag components.

(1) Since the vehicle has attained a constant temperature, its "dU/dt" equals zero.
(2) is zero because the speed is constant.
(3) is zero because the road is horizontal.
(4) The "simple compressible" car has a constant volume.
(5) The sum of heats to the car equals zero.

Our energy equation becomes:

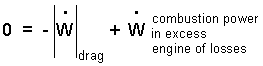
(3)Drag represents "work-like" energy LOSS of the car.

The "work" term of original energy equation consists of two components. Work arrives to the car delivered by the combustion of the fuel/air mixture that passes through it. Some of the combustion power is expended by moving parts of the car, especially its motor and tires. We assume the combustion work to exceed the losses by 160 kW.

In horizontal travel the power of combustion passed to the car passes to the surround environment. To write the term for "work passage to the environment" is awkward. In general work can be positive or negative. Thus to write "-W" is insufficient to describe loss of energy. Our choice is "-|W|" which means "energy loss of a system by a work mechanism.

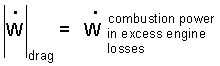
(4)Combustion power to the speeding car minus car "inside friction" losses is lost to the friction of moving through air; drag.

We represent that work rate a being the negative of an p