| THERMO Spoken Here! ~ J. Pohl © | TOC NEXT ~ 166 |
Tank, Spring and Heater
Initially the temperature of the everything is uniformly 300K and the water in the stand-pipe resides at (1). The spring is compressed, it holds the frictionless piston to the left. At time, t = 0+, the heater is turned on. It deliver 6 kilowatts of thermal energy to the air.
Assume there is zero heat to the surroundings and that all parts of the system remain at 300 K with the exception of the air. The final state occurs when the water level in the stand-pipe is 8 meters higher.
At what time is State (2) attained? The rate form of equation is needed. We will take the system to be the air, the piston, the spring and the water.
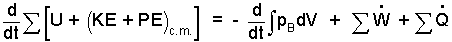 |
(1) 1 |
If the heating coil is excluded from the system, the 6 kW is heat (If the coil is included, the 6 kW is work). Compression work occurs at the water/air interface. The system "backs off" the atmospheric pressure-force. That is, pB equals patm. Next we separate variables and set up to integrate:
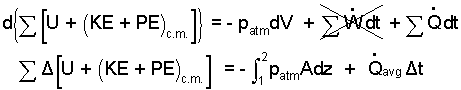 |
(2) 2 |
There system has four components: air, piston, spring and water. All kinetic energy changes are zero. Only the water has a potential energy change.
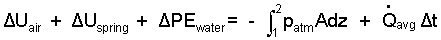 |
(3) 3 |
Relations for energy changes for the air, spring and water are:
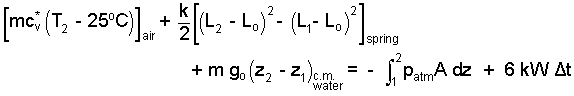 |
(4) 4 |
It is convenient to put some numbers into this equation. The only information about State (2) is the second elevation of the water in the stand pipe. We write a mass equation for the water with moving boundaries at the piston face and air/water interface. We apply a Leibnitz differentiation.
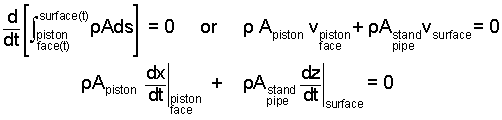 |
(5) 5 |
We separate variables and integrate again. Powerful method, easy case.
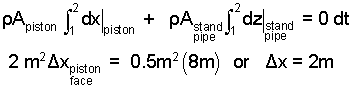 |
(6) 6 |
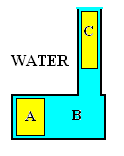
Thus the spring is compressed two meters. Water is displaced at the piston face. Draw a picture to be certain about the change of potential energy of the water.
PEwater,2 = PEwater,C + PEwater,B
PEwater,1 = PEwater,A + PEwater,B
PEwater,2 - PEwater,1 = PEwater,C - PEwater,A
ΔPEwater = mwatergo[(z - zo)c.m.,C - (z - zo)c.m.,A]
It is our prerogative to select a zero datum for potential energy. We set:
zc.m.,B = zo whereupon: ΔPEwater = mwatergo(12 - 0)m
We take the centerline of the piston as the zero datum for potential energy of the water. Thus the difference of potential energy equals the potential energy of the new water in the standpipe.
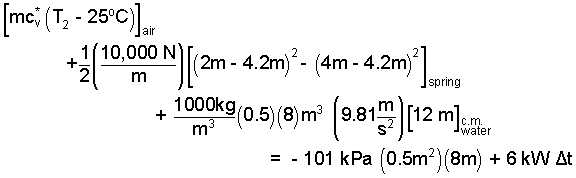
| (7) 7 |
By checking, we see contributions of the spring and the water are correct. We turn those expressions into numbers.
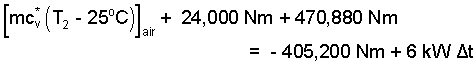 |
(8) 8 |
Our next task is to determine T2. The mass of air is constant. Its pressure, temperature and volume increase as it is heated. The second pressure can be calculated. In State (2) the force of the air on the right face of the piston equals the force of the water and of the spring that acts on the piston's right face. This will require the momentum equation for the piston. (We've done that before.)
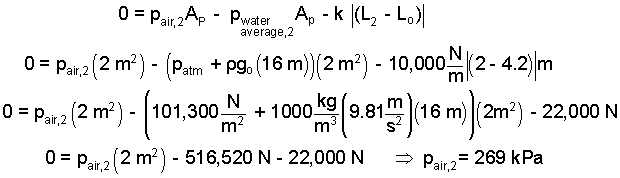 |
(9) 9 |
Next we calculate the mass and then use it to calculate the second temperature.
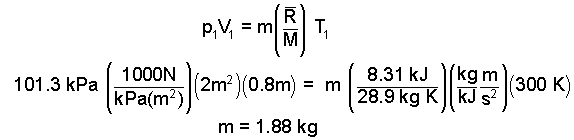 |
(10) 10 |
The piston displaces two meters to the right. Thus the second volume of the air is: V2 = (0.8 + 2.0)(2) m3. Returning to the ideal gas equation:
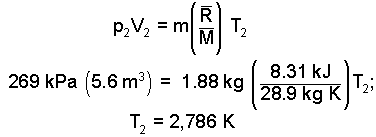 |
(11) 11 |
This required temperature is VERY high. The design won't work."
Tank, Spring and Heater
Initially the temperature of the everything is uniformly 300 K and the water in the stand-pipe resides at (1). The spring is compressed, it holds the frictionless piston to the left. At time, t = 0+, the heater is turned on. It deliver 6 kilowatts of thermal energy to the air.
The final state occurs when the water level in the stand-pipe is 8 meters higher. At what time is State (2) attained?
Premise presently unwritted!