Candle Beneath a Piston

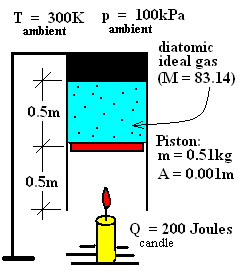
The event of this discussion is an "idealized heating" of an ideal gas inside an "idealized piston/cylinder" assembly. You must believe in make-believe! The theoretical, frictionless apparatus assures a constant pressure process of the ideal gas. Conditions of the figure correspond to the instant the candle is lighted. When the candle has burned completely it will have provided 200 Joules of heat to the diatomic ideal gas (M = 83.14) contained.

To Begin, calculate the mass of the ideal gas contained.
♦ We apply the momentum equation in the vertical to the piston to determine the pressure of the contained gas.

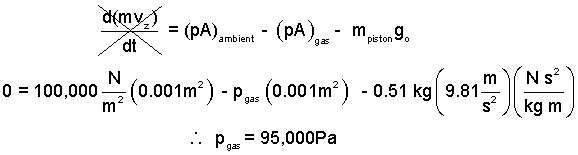
(1)1

Knowing the pressure, the ideal gas equation will yield the mass.

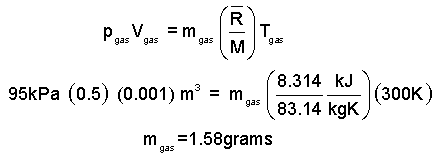
(2)2

Calculate the heat that will cause the piston to fall on the candle.
♦ We write an increment form energy equation with the contained gas as our system. The slow process will proceed at constant pressure. The boundary pressure, p_B, of the work term will equal the gas pressure, p_gas. The initial kinetic energy and final kinetic energy of the gas equal zero.

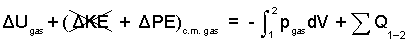
(3) 3

The potential energy change is expressed as shown. The work of the gas equals its pressure times area over boundary sections that move (the piston face). Boundary pressure at the piston face equals the gas pressure, p_gas, which is constant in the piston/cylinder arrangement. The work equals -Δ(pV)_gas.

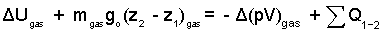
(4) 4

Inspecting the above equation, we see the term ΔU_gas, left-of-equality and -Δ(pV)_gas, right-of-equality. A convenience occurs when we add Δ(pV)_gas to each side of the equality.

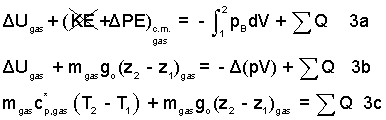
(5) 5

Above, we see that the work and internal energy change combined to become the enthalpy change of the event. We need T₂. The mass of the gas is constant and so is the pressure.

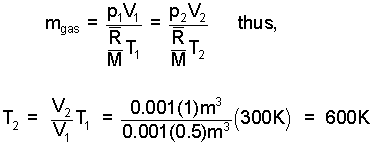
(6) 6

The change of potential energy of the gas is small but we calculate it to show how it is done.

If we take the top of the cylinder as a "z = 0" datum, then the initial elevation of the gas center of mass is: z_{c.m. gas,1} = - 0.25 m. The final elevation is: z_{c.m. gas,2} = - 0.5 m. Being an ideal diatomic gas, the specific heat at constant pressure is:

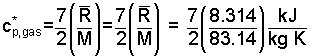
(7) 7

Now we are ready to put the numbers into the equation.

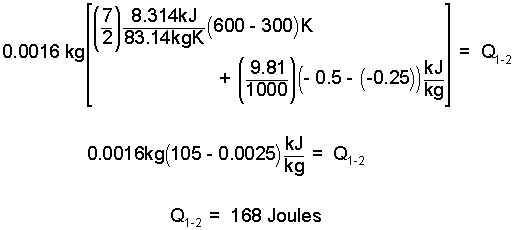
(8) 8

So, 168 Joules are required and the candle delivers 200. We conclude the piston will move downward and fall from the cylinder.