| THERMO Spoken Here! ~ J. Pohl © | TOC NEXT ~ 157 |
3.17 Heat and Work Sign Conventions
While every thermodynamicist uses only one sign convention, it might not be the same as another uses. The clearest way to state your sign convention is by a quick sketch. The figure shows three conventions for the purpose of discussion.
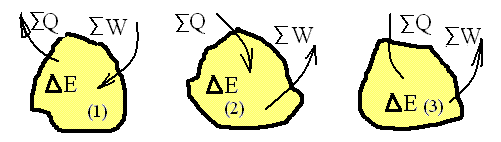 |
Which is Wrong? Are any of the sign conventions wrong? If so, why?
♦ Both 1) and 2) are complete. Work or heat are noted by an arrow crossing the system boundary which indicates the positive interaction (arrow head pointing to the system) or negative interaction (arrow head pointing away from the system). One is at liberty to define transfers arbitrarily. However, Convention 3) is wrong because it is incomplete, the arrow of heat, ΣQ, has no arrow head. (Notice: Our results would be valid were no summation signs, Σ used. However the heat and work of events ARE sums. To consistently write ΣW and ΣQ helps one avoid mistakes.)
Does the energy equation, ΔE = ΣW + ΣQ, apply to (1) or (2)?
The energy equation for system 1) is: ΔE = ΣW - ΣQ
The energy equation for system 2) is: ΔE = -ΣW - ΣQ
Consequently ΔE = ΣW + ΣQ does not apply to either (1) or (2).
Given: ΣW = 6 kJ and ΣQ. = -10 kJ. Calculate ΔE using convention (1) then using convention (2).
♦ 1) ΔE = ΣW - ΣQ, so ΔE = [6 - (-10)]kJ = 16 kJ
♦ 2) ΔE = -ΣW + ΣQ, so ΔE = [-6 - 10]kJ = -16 kJ
The energy equation representing the adopted sign convention of this writing is:
ΔE = ΣW + ΣQ
From the equation we conclude that heat and work are positive for events wherein their respective energy transfers contribute energy to the system. Thus the schematic system has both arrows directed into the system.
3.11 Heat and Work Sign Conventions
While every thermodynamicist uses only one sign convention, it might not be the same as another uses. The clearest way to state your sign convention is by a quick sketch.
Which, of the sign conventions shown, if any, is wrong and why?
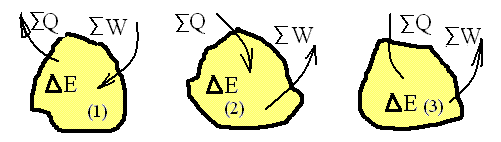 |
The depiction “(3)” is incomplete. Heat as “to or from ” the system
is not indicated. Therefore “(3)” is wrong by omission.