| THERMO Spoken Here! ~ J. Pohl © | TOC NEXT ~ 102 |
Roof-Top Exit
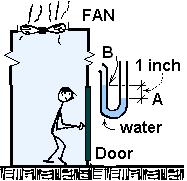
A building 1200 feet in height will have a doorway for rooftop exit. Air interior to the building will be maintained at 70°F and prevailing local pressure. The worst case of air outside in a light breeze is 40°F and 14.7 psi.
On the roof is a powerful fan which when turned on, will act to force air from the building and into the outside air. At ground level the building has a typical door which we assume to be air-tight such that air cannot leak past the seals along its sides, top and bottom. Furthermore assume the entirety of the rest of the building has no "leaks" or paths for air to enter or leave the building - the single exception is the exhaust duct of the fan on the roof.
Establishment of the Initial Condition: Originally the fan is not operating and the pressure inside the building equals that of the atmospheric air outside. When the door is closed, the fan begins to operate and the pressure within the building begins to decrease. After the fan operates for an extended time, the pressure within the building will cease to decrease. The pressure inside of the door will become some constant pressure (depending upon the power and design of the fan) that is less than the pressure. To open, the door swings outward.
Technical Talk: The author states the inside pressure is 1 inch of water (vacuum). The statement, "1 inch of water," has special meaning. The "1 inch," is not a pressure; it is the height of a column of water in a manometer. The manometers measure differences in pressure, that is:
The sketch shows the building with a person standing inside, in front of the roof-top door which measures 3 ft. by 7 ft.
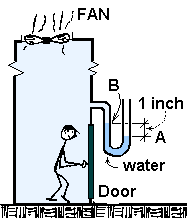
Determine the force required to open the door.
♦ First we must determine the pressure inside the building. To proceed we must
know the pressure somewhere. It is logical to assume the outside pressure to be standard atmosphere.
Thus the pressure of the air at "A" (just above the water in the right leg) is one atmosphere. The pressure
at "A" but just under the water surface is also one atmosphere. The pressure of the water in the left leg at
the level "A" is also one atmosphere. Finally, the pressure of the water (and air) at level "B" in the left leg is
less than at level "A" by "one inch of water." We write and solve the hydrostatic equation:
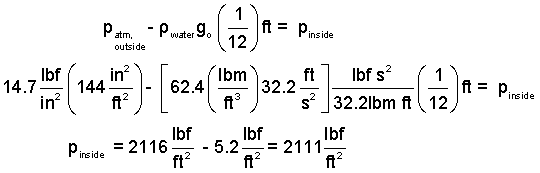
| (1)1 |
The above calculation provided both pinside and poutside. The next task is to calculate the force that must be applied by the person's hand to open the door.
Two views of the door as a FBDare shown below. The door is view from above. Below left, the distributed forces of air are shown. Below right the distributed forces have been replaced by a equivalent single forces.
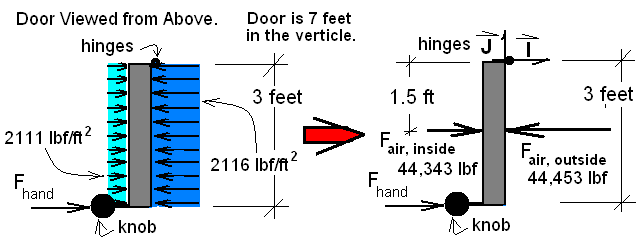
The door will pivot about its hinges as it swings outward. The sum of moments consists of three terms.
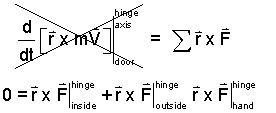
| (2)2 |
We will use a vector approach. The sketch above right shows the I and J of our vector basis. The K is directed upward.

|
(3) 3 |
The force calculated is 55.6 lbf. Thus it is likely you could open the door.
Roof-Top Exit

A building 1200 feet in height will have a doorway for rooftop exit. Air interior to the building will be maintained at 70°F and prevailing local pressure. The worst case of air outside in a light breeze is 40°F and 14.7 psi.
On the roof is a powerful fan which when turned on, will act to force air from the building and into the outside air. At ground level the building has a typical door which we assume to be air-tight such that air cannot leak past the seals along its sides, top and bottom. Furthermore assume the entirety of the rest of the building has no "leaks" or paths for air to enter or leave the building - the single exception is the exhaust duct of the fan on the roof.
Premise presently unwritted!