Two Tanks

Each tank is square in cross-section and has a valve for filling with water (or venting of air) at its top. The tanks are connected at their bottoms by a pipe with a valve.

Two cases are to be studied. The sketch shows the setup for both: all valves are closed, the depth of water in tank A is 5 meters and the water depth in tank B is zero. Events initiate when valves are opened. For each event, calculate the final depth of water in each tank. Since the events take a long time, temperature is constant.

Case I: If all valves are opened, what will be the final depths of water in the tanks?
♦ We take the system to be water "above" the zero level of both tanks. Since the density of water is constant, the mass of water initially above H = 0 will equal the mass above H = 0 finally.

Δm = 0 or m_water,2 - m_water,1 = 0

The mass equation is expanded to account for the two tanks:

[m_A,2 + m_B,2] - [m_A,1 + m_B,1] = 0

We expect the final depths of water in the tanks to be equal at H₂. So we write each mass as: ρ_waterA_tankH. The tank areas are known:

Area A = 9m², Area B = 4m² and Also H_A,1 = 5m.

Place these facts into the mass equation:

[ρ_water(9m²) H₂ + ρ_water (4m²) H₂] - [ρ_water (9m²)(5m) + 0]= 0.

The above is a mass equation and each of its terms has the dimension mass, [m]. However the equation has been reduced to the point of containing a single unknown - the second height we seek. Thus now is the time to manipulate the equation algebraically for a solution. Reduce by division by ρ_water:

9m²H₂ + 4m²H₂ - 9m²(5m) = 0

Which gives us:

H₂ = (45/13) meters.

Case II:Suppose from the initial condition, only valves 2) and 3) are opened, what then will be the second depth?

Valve 1) is left closed and air is trapped in tank B. This will influence the final depths. We will study two systems: i) all of the water and ii) the air in tank B. For the water, by reasoning as above but with the second depths, we have:

9m²H_A,2 + 4m²H_B,2 - 9m²(5m) + [m_air,2 - m_air,1] = 0

The mass equation for the air is:

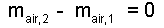
(1) 1

The air is compressed, apply the Ideal Gas Equation to it:

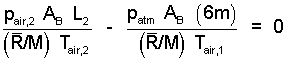
(2) 2

The original depth of air in Tank B from the top was 6 meters. As water flows into tank B, the depth decreases to L₂ which equals 6m - H_B,2. The second time is a long time after the valves were opened. Consequently T_air,2 = T_air,1. These facts are applied to obtain a final equation for the air. Just below that equation is written the equation for the water:

[p_air,2(6m - H_B,2) - p_atm(6m)] = 0

[9m²H_A,2 + 4m²H_B,2 - 9m²(5m)] = 0

These are two equations and we see there are three unknowns: p_air,2, H_A,2 and H_B,2. The added equation we need is the hydrostatic equation written from the water surface in Tank A through water to the water surface in Tank B. We expect H_A,2 will be greater than H_B,2. With that, the equation becomes:

p_atm + ρ_waterg_o(H_A,2 - H_B,2) = p_air,2

The event is physical, it has an answer and only one answer. The three equations above are based upon sound principles; by a double-check, they are correct. There being three unknown quantities, three independent equations are sufficient for solution. Solve the set and you'll get the answer.