| THERMO Spoken Here! ~ J. Pohl © | TOC NEXT ~ 99 |
First Equestrian Ascent
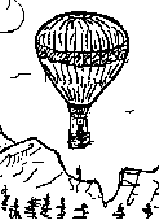
At the World Fair in Paris (1798) the crowd watched curiously as Louis Testu-Brissy assembled his hot air balloon with its platform-shaped gondola. His aides lighted the "lifting flame," the balloon inflated, became spherical and then, to the astonishment of all, the balloon and horse (with Louis astride) slowly ascended high above the fairground.
The information of the sketch (below right) depicts the balloon, horse and everything in air, just above the lift-off platform, an instant after it left the ground. The mass of the horse/equipment and the diameter of the balloon were 500 kilograms and 20 meters, respectively. Centers of mass of system components are shown.
Calculate the least temperature of the air within the balloon for the ascent to commence.
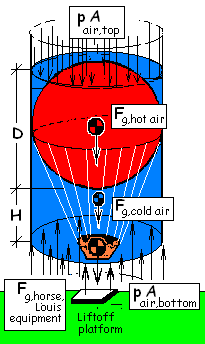 ♦ Having experience in analysis, we select our system as a cylinder of air that encompasses everything. A sketch, free-body-diagram is shown (right). At ground level the pressure of air is atmospheric pressure. The balloon is open at its bottom. Newton's 2nd Law applies, the vertical component of the momentum equation is:
♦ Having experience in analysis, we select our system as a cylinder of air that encompasses everything. A sketch, free-body-diagram is shown (right). At ground level the pressure of air is atmospheric pressure. The balloon is open at its bottom. Newton's 2nd Law applies, the vertical component of the momentum equation is:
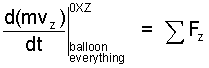
| (1) 1 |
The balloon, before it commences to rise, is supported by the lift-off platform. The sketch shows a spherical mass of air inside the balloon which is hot as a consequence of the "lifting flame." That "hot air" has a uniform density (at lift-off), ρhot.
Around the "hot air" inside of the balloon are balloon materials, equipment, Louis and the horse - we notate these masses, collectively as: mequip. Filling the remainder of space of the cylinder is cold atmospheric air with constant density, ρcold.
At the moment of lift-off the momentum of everything is zero. Expanding the sum of forces (right side of Eqn-1), the momentum equation, (0 = ΣF) yields:
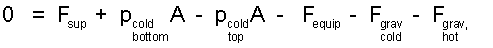
| (2) 2 |
The pressure difference, bottom minus top, of the cylindrical system is grouped and all air masses are written as densities times volumes. Also above, we have expressed the mass of the horse, equipment and Louis (combined) as an effective density times its volume.
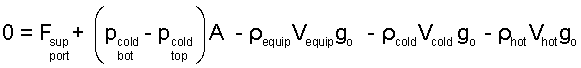
| (3) 3 |
Next the hydrostatic principle is applied to represent the pressure difference of atmospheric air, bottom to top of the system. A constant atmospheric density is assumed. The pressure difference needed above is:
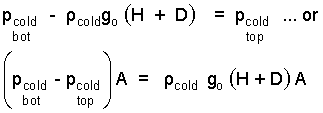
| (4) 4 |
But (H + D) A equals the entire system volume which is the sum of the volumes of its parts. We use this fact to alter the result immediately above:
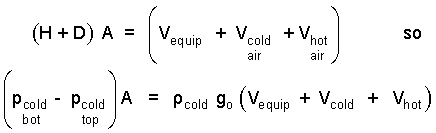
| (5) 5 |
Substitute the above to be the second term of the momentum equation (1).
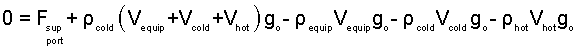
| (6) 6 |
Check the equation again. Then rearrange the terms (Yes, this time do some algebra).
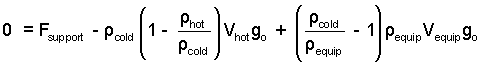
| (7) 7 |
Check the algebra. The density of the cold air is miniscule in comparison the the effective density of the equipment. Change (ρV)equip to mequip. Apply the ideal gas equation to express the air densities ( (ρ = p/RT)
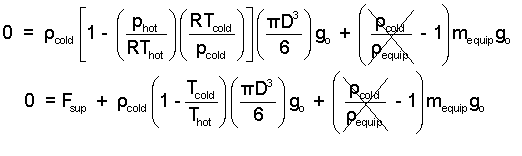
| (8) 8 |
Our interest has been the "moment of lift-off." That is when Fsupport becomes zero. The equipment mass is 500 kg. The balloon diameter is 20 meters. A reasonable value for the density of atmospheric air (at 300K) is 1.2 kg/m3.
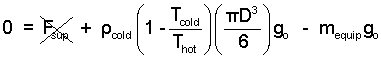
| (9) 9 |
Thus upon calculation we determine the "lifting temperature" must be at least 333K (60°C).
First Equestrian Ascent
At the World Fair (Paris ~ 1798) the crowd watched curiously as Louis Testu-Brissy assembled his hot air balloon with its platform-shaped gondola. His aides lighted the "lifting flame," the balloon inflated, became spherical and then, to the astonishment of all, the balloon and horse (with Louis astride) slowly ascended high above the fairground.
Premise presently unwritted!