THERMO Spoken Here! ~ J. Pohl ©

TOC     NEXT    ~   95

Majic Fountain

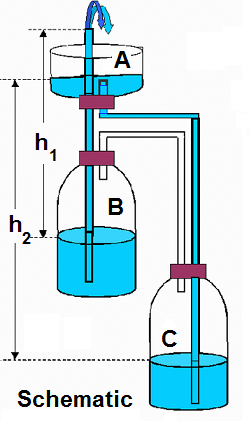Three glass bottles (A, B, and C) each contain air and water with a free surface. The bottles are connected by tubes; air is trapped within bottles B and C. It is claimed, for the "instance" depicted, that a jet of water issues at the top (bottle A). Use the height differences of water surfaces (h₁, and h₂) with the Bernoulli Equation, to state the velocity of the jet algebraically.
==============================================

Discussion: This problem was encountered "online." The image above-right is a download. Upon inspection one might wonder, by its nature, does the apparatus produce a jet? It appears the jet would be transitory. It is unclear where the jet of water lands. Surely the jet is not perpetual. We set our goal to answer the problem question posed and to understand how (if?) the apparatus functions. It would seem the apparatus would exist in some initial state and that an event would cause the jet. Take that path to investigate.

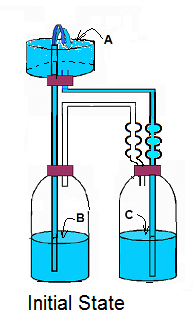Initial State and Event: Prior to its operation the apparatus must have been "set-up." To operate, the jars, water, con­tained air and tubes must have been cast in an "initial configuration."

The figure "Initial State" shows a possible, assumed initial, stable circumstance for the bottles, water, air and tubes. The water surface at A is tidied-up a bit. To be connected by rigid fixed-length tubes permits the event. The figure shows "extendable" connections. We assume, for a jet to happen, the bottles would be as Initial State then changed, the "Event," to "Schematic" by prompt lowering of bottle C which is permitted by the extendable tubes.

It would seem analysis of this event would confirm or refute the jet.

Prove: (-1) x (-1) = 1

Most of us use this fact without thinking about it.

Premise presently unwritted!