Wilma's Surge

Persons who have experienced the eye of a hurricane witnessed its calmness, its winds with low velocities and also high water levels. Some call these "high tides" but the water levels are not strictly tidal, not related to location of the moon only. A component of the high water level within a storm center is appropriately called "storm surge."

In a hurricane, great masses of atmospheric air move in a gyre or great circle across the sea. The winds converge toward the storm center then spiral upward to high altituides. As a consequence the ground-level ambient pressure at its center, called its "eye," becomes lower than normal atmospheric pressure. Still, around it and at distances away from the center, over a vast circular remainder of the sea, the usual atmospheric pressure acts. So the atmospheric pressure acting on sea surface at a distance pushes water toward the low, storm-created pressure in at the storm center. This conponent of increase of water level is called the "surge." It is stated that the pressure in eye of Hurricane Wilma was 882 mbar.

Estimate the height of water surge within the eye of Hurricane Wilma.
♦ To fashion a solution we imagine a manometer that extends from far out to sea where the pressure is atmospheric (1013 mbar) all the way to the center of the hurricane, to its eye, where the pressure is 882 mbar (see sketch).

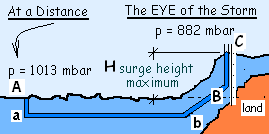
The sketch depicts a long pipe (A-a-b-B-C) open-at-both-ends and full of sea water. The beginning, "at a distance" point A is selected far out to sea where we know the pressure is standard atmospheric. To use of the hydrostatic principle we imagine how pressure of the sea water within the pipe changes along points on the path (inside the pipe) from A to C.

From location A the path proceeds downward to point a and the pressure increases somewhat. For points along the horizontal length from a to b, the water has the same depth and the same "slightly-greater-than-standard-atmospheric" pressure. In proceeding upward from b to B the pressure decreases as much as it increased between A and b (remember, p_a = p_b). Thus the pressure at B equals the pressure at A ~ standard atmosphere or 1013 mbar. Point C (at the water-to-air interface) has the pressure, 882 mbar. By the hydrostatic principle, starting at B and proceeding upward to C pressure decreases; the equation is:

p_B - ρ_{sea water}g_o H_surge = p_C

(1) 1

Although the above equation could be re-written to have H, alone and left of equality, resist premature algebra. Keep this (and other) equations intact. Let the equation flow down the page until it contains nothing but numbers and H. Then apply algebra.

1013 mbar - (1025 kg/m²) (9.81 m/s²) H = 882 mbar

(2) 2

It is likely weather forecasting will always use the pressure unit, Bar. So learn to do these unit conversions.

101,300 N/m² - (1025 kg/m³) (9.81 m/s²)(N s²/kg m) H = 88,200 N/m²

(3) 3

Note the group (Ns²/kgm) is dimensionally [1].

101,300 N/m² - (1025)(9.81)(N/m³)H_surge = 88,200 N/m²

(4) 4

The unknown height, represented by H, has no units. When H is solved for as a number, it will automatically have the correct units (otherwise there has been a mistake.

H_surge ≥ 1.30 meters (~4.3 feet)

(5) 5

The answer means that nowhere along the coast near the landfall of Wilma (barring special circumstances) was the depth of water less that 1.3 meters above its typical the sea level height. Witnesses of Wilma reported much greater depths. One reason our number is low is that we ignored the dynamic effect of the winds blowing the shallow near-shore waters.