| THERMO Spoken Here! ~ J. Pohl © | TOC NEXT ~ 86 |
Off-Shore Natural Gas

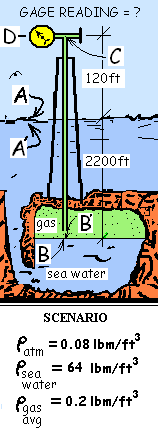
An image of an off-shore natural gas well is shown. In normal operation natural gas flows from a gas reservoir beneath the ocean floor upward through pipes to the production rig then through pipes leading to shore facilities. Occasionally valves are closed such that the gas flow is stopped. The "stopped or no-flow" condition is our interest.
The schematic sketch below right depicts the basic "stopped flow" configuration. Also some representative average densities of the substances involved are provided. Some reference points for our analysis have been added. Use the information provided to calculate the approximate reading of the pressure gage (G.R.) located at the well head, at location: "D."
♦ The procedure we will apply is to identify a place where we know the pressure, then apply the hydrostatic principle (successively) to obtain an equation in which the G.R., the reading of the pressure gage at the wellhead, is the only unknown quantity.
We select to start at location A. We know the pressure at point A (in air at the surface of the sea) to be atmospheric pressure.
| patm = pA | (1)(1) |
The pressure at A', a location closely below A in sea water, is also atmospheric since pressure change across a flat gas-to-liquid interface is zero.
| patm = pA' | (2) (2) |
Next we consider the pressure at location B. The pressure at B is greater than the pressure at A' by the pressure increase that occurs top-to-bottom in a column of sea water 2200 feet tall. Pressure increases for all points in moving downward from A'. Moving to B produces an increase of pressure of:
| ρsea water go (2200 ft) | (3) (3) |
Let us add this amount of pressure increase to both sides of the previous equation:
| patm + ρsea water go (2200 ft) = pA' + ρsea water go (2200 ft) | (4) (4) |
Now we do two steps. First, recognize that the sum of terms right-of-equality equals the pressure in sea water at location B. And as before, the pressure just above (across the liquid-to-gas interface) at location B' is the same number. Consequently, the equation we are developing can be written as:
| patm + ρsea water go (2200 ft) = pB' | (5)(5) |
Natural gas fills the well pipe from the location B' vertically through (2200 + 120) or 2320 feet to the location inside the pressure gage, at C. The pressure of the gas at C is less than at B' by the pressure difference, bottom-to-top of a column of natural gas 2320 feet tall, that is, by the amount:
| ρsea water go(2320 ft) | (6) (6) |
Since the pressure in gas at D is less than at B' we will subtract this number from left-of-equality and (omitting one step) we will simply write the pressure right-of-equality as PC. Our next intermediate result is:
| patm + ρsea water go (2200 ft) - ρgas go (2320 ft) = pC | (7) (7) |
Now we deal with the gage. The pressure "inside of" the gage is pC. The pressure "outside of" the gage, in ambient air, is pD. The gage reading, G.R. equals the difference between these pressures, that is:
| pC - pD = G.R. or G.R. = pC - pD | (8) (8) |
Therefore when we subtract G.R. from left-of-equality above and its equivalent, pC - pD from right-of-equality, we obtain pD, the ambient pressure "outside of," beside the gage.
Point D is in a location in atmospheric air immediately outside and at the same elevation as the gage. Now construct an equation containing the gage reading, GR. Begin at point A where the pressure is known to be one atmosphere.
| patm = pA | (9) (9) |
At B (in sea water) the pressure is greater than at A by the amount of pressure added by a column of sea water 2200 feet in height. The pressure in the gas also equals, pB
| patm + ρsea water g (2200 ft) = pB | (10) (10) |
The point C is directly above B. Pressure, starting at B will decrease steadily with positions above B. The pressure at C is:
| patm + ρsea water g (2200 ft) - ρgas,avg g (2320 ft) = pC | (11) (11) |
The point D is the ambient pressure outside of the gage. The gage reading tells us the difference in pressure, pinside- poutside. Thus if we subtract the gage reading (GR) from pC we get pD.
| patm + ρsea water g (2200 ft) - ρgas,avg g (2320 ft) - GR = pD | (12) (12) |
We see our equation has two unknown terms: pD and GR. Lets return to point A where the pressure is patm.
|
patm + ρsea water g (2200 ft) - ρgas,avg g (2320 ft) - GR + ρair g (120 ft) = patm | (13) (13) |
Now we have one equation and one unknown. Subtract patm from both sides. Put numbers into the equation.
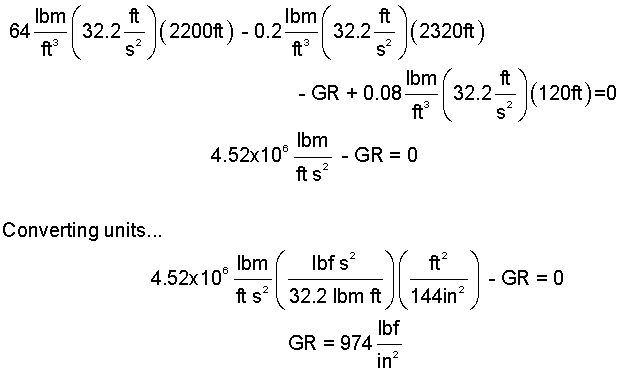
Off-Shore Natural Gas

An image of an off-shore natural gas well is shown. In normal operation natural gas flows from a gas reservoir beneath the ocean floor upward through pipes to the production rig then through pipes leading to shore facilities. Occasionally valves are closed such the gas flow is stopped. The "stopped no flow" flow" condition is our interest. Use the information provided to estimate the well-head pressure of the natural gas.
Premise presently unwritted!