Yacht and Sea Buoy

Two dimensional motion.

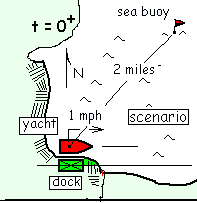
A yacht sails to the east from a dock with a speed of one mile per hour. Two miles northeast of the dock a sea buoy is anchored. The event starts at t = 0⁺ with the yacht position and velocity and the position of the sea buoy as indicated in the scenario sketch (right).

When will the yacht pass closest to the Sea Buoy?
What will be the distance from the yacht to the buoy at that time?

♦ A vector diagram is drawn (below right) with its origin placed at the dock, its coordinates and unit vectors (I and J) indicated. The yacht is shown a distance from the dock at an intermediate and arbitrary time of the event, t = t^*.

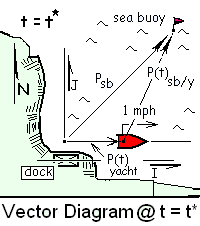The equation relating position of the dock, yacht and sea buoy (sb) is:

P_yacht(t) + P_sb/y(t) = P_sb

It is a good habit to include time dependence by writing "(t)" with properties that change with time. This is a 2-D vector equation.

When it is solved it will yield two pieces of information. When writing an equation it is helpful to do the easy parts first. Of the three vectors we need, position of the buoy is the easiest to write.

It is a good habit to include time dependence by writing "(t)" beside event characteristics that change with time. The vector equation relating positions of the dock, yacht and buoy is:

P_sb = 2[cos(45°)I + sin(45°) J] mi

The yacht, originally at the origin, is moving East at 1 mph for all t > 0⁺.

P_y(t) = 0 I + 0 J + 1 mph· t I

Putting these results into the equation (with time in hours):

t I + P_sb/y(t) = 2 [cos(45°) I + sin(45°) J] mi

So everything is known except P_sb/y(t).

P_sb/y(t) = (√2 - t) I + √2 J

The distance between the yacht and buoy, D(t), is the length of this vector:

D(t) = |P_sb/y(t)| = [ (√2 - t)² + (√2)²]^1/2 miles.

Next we write the above D(t) in a "completed square" form:

D(t) = [(t - √2)² + 2]^1/2miles.

So "D(t)" is least when t = t^* = √2 hours. And the distance is:

D*( t^* = √ 2 hours) = √ 2 miles.