THERMO Spoken Here! ~ J. Pohl ©

TOC NEXT ~ 28

Scissor-Jack

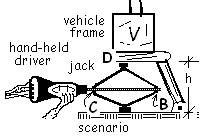
This sketch is a physical scenario. It depicts what will happen.
Looking at it closely, we anticipate the lift-rate of the scissor-jack 
will vary during any lift with constant input rotation.

A scissor-type car jack is shown. Member BC is threaded such that when it is rotated by the hand-held driver, its length, the distance |BC| shortens. By the mechanism this causes the top of the jack (with elevation, h(t)) to move upward.

The lead of the threaded bar BC is 0.1 cm/rev, meaning one rotation of the screw shortens the distance |BC| by 0.1 cm. Suppose, (in the position shown - dimensions given below), the driver rotates member BC at = 200 revolutions per minute.

Calculate the upward velocity of the top of the jack, point D.

The first step is to transform the scenario into a system sketch, select an origin with X and Z coordinate directions. Also set up an I - K vector basis. Add appropriate notation.

A scenario becomes a system sketch when 
coordinates, dimensions, a vector basis 
and notation are added.

For this jack, there are two independent vector paths from the ground (origin) to its top, D. Write both paths. Then since both paths go to the same place; equate them.

By the vector diagram, one path from the origin to D is:

OD = OA + AD

(1) We see this is true; visually.

A second path from the origin to "D" is:

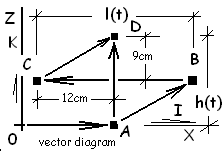
OD = OA + AB + BC + CD

(2) 2

But the first path equals the second, so we have:

OA + AD = OA + AB + BC + CD

(3) 3

The equality of paths shows the vector OA to be redundant, meaning we could have started at A.

AD = AB + BC + CD

(4) 4

This vector equation is implicit, and simple in form. By visually tracing the paths, we see that it is correct. Next, using the numbers, unit directions and geometry, we represent as much of the implicit equation, explicitly. Let's walk through the steps, term by term (left to right) through our equation.

About the first vector, AD. Obviously the length of that vector, |AD|, will change as the jack operates. The purpose of the device is to increase the height (call it h(t)) of what is being jacked upward. So write:

AD = |AD| K

(5) 5

Thus

AD = h(t) K

(6) 6

The next vector, AB (right of equality), has a constant length (15cm) but its direction changes in time. We use trigonometry with the angle, θ(t), to specify its direction:

AB = 15cm [cosθ(t)I + sinθ(t)K

(7) 7

The threaded rod extends from B to C. Its vector direction is "-"I and the vector length (at this instant), is l(t), so:

BC = l(t)[-I]

(8) 8

Leave this as it is.

Vector CD is the same length and parallel to vector AB.

CD = 15 cm [cosθ(t)I + sinθ(t) K]

(9) 9

Finally, enter these explicitly written vectors into the initial implicit equation.

h(t)K = 15cm[cosθ(t) I + sinθ(t) K] - l(t) I + 15cm[cosθ(t) I + sinθ(t) K]

(10) 10

By vector algebra, this condenses to:

h(t)K = 30cm [cosθ(t) -l(t)] I + 30 sinθ(t) K]

(11) 11

The steps are always the same. We used vectors to keep things together, now we separate the motion into its components by vector multiplying the equation by I then K. From these components respectively, we obtain:

0 = 30 cosθ(t) - l(t),

(12) 12

and,

h(t) = 30 sinθ(t)

(13) 13

Another piece of information relates to the change of length, |BC| which we have labeled l(t). The equation for l(t) is:

l(t) = l_o - (0.1cm/rev)α(rev/min)t

(14) 14

The three equations above are independent. Since we need velocities, we differentiate those equations with respect to time. One could form the difference quotient of the of the equations then take the limit. Better to learn what the derivative of sine and cosine functions are and use them.

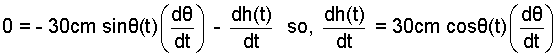
constants_2

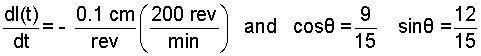
Also included (above right) is that we know the values of the cosine and sine for the position of interest. Solution of the three equations yields:

dh/dt = 15 cm/min

(17) 17

Every step is included. Vectors put the spatial aspects in precise form. You can solve similar problems. All you need is patience and a large sheet of paper.