THERMO Spoken Here! ~ J. Pohl ©

TOC NEXT ~ 68

Water Pumped Vertically

Displays of "water-and-light" at hotels in Las Vegas involve quite complex pumping, piping and lighting systems. The sketch below right depicts the components (reservoir, submerged motor, pump housing and piping) of one such cosmetic water display.

Two aspects a pumping event is its transient and its steady operation. For our simple analysis we assume the instant electric power is supplied to the pump that water passes through at a constant volume rate, at a constant number of gallons per second. In addition we assume ideal operation, we assume there is no friction whatsoever.

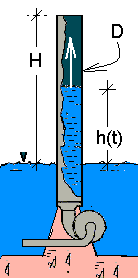Upon starting the pump will commence (at a constant volumetric rate of flow ) to fill the stand-pipe. As the water level rises the power required by the pump must increase. This trend continues until the water attains the height, H, whereupon water will begin to spill from the pipe. System operation after the water height is, H, is steady.

Calculate the transient and steady power required of the pump.
♦ Below we analyse the pump event useong two distinct system representations. The system mass equation and energy equation apply in a "rate" form.

Mass Equation: Summation signs, a good habit, remind use to include all instances of "system, in or out."

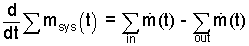
(1)1

Here there is one entrance and one exit. Terms of the mass equation can be written explicitly.

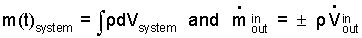
(2)2

Energy Equation: This energy equation is long because it contains representational terms for all types of interaction. It is a load to write out seen to be useful as non-applicable terms are removed. We write it out every time because it contains all terms that might apply.

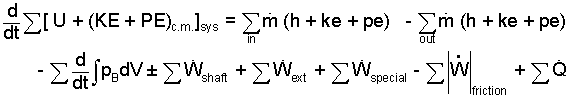
(3)3

Equations 1,2 and 3 contain "all of the terms" in general. The equation applies by reduction to the system perspectives, open, closed or unsteady, by its specialization by striking out the inapplicable terms.

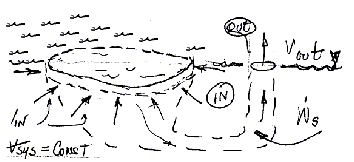
Constant volume system is open
with an infinite, “free surface”
entrance and a “finite” exit.

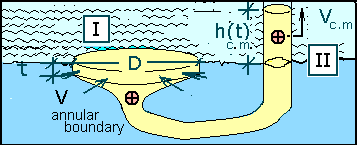
Open System Perspective: The system is the water that passes through the pump. The system is not "parts of the pump, pipes et al." The sketch to the right represents our system as the constant volume of water contained within an imaginary, dotted boundary. Water enters the system across its "in" boundary, at all places on the perimeter of a large circular annulus shown as a "dashed" ellipse. The pump (not shown) drives water from the space to an exit and "up the pipe." The pump supplies power to the water. It is represented schematically as its power input, W_s. We reduce the mass and energy equation terms proceeding "left to right" as they appear in the equation.

Their is a single mass of the system, (m), and it is constant. The system energies KE and PE relate to the motion and elevation of the center of mass of the system. The center of mass does not move, hence the derivatives of KE and of PE are zero. The left-of-equality terms are as follows:

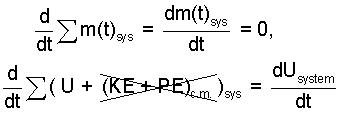
(4) 4

The system has only one entering stream and one leaving stream. Further steps for the mass equation are:

(5)5

Using the reduced mass equation (above) we look at the first two terms (right-of-equality) of the energy equation.

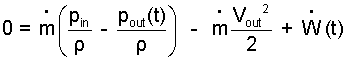
(6) 6

The next term is the system work as a consequence of change of volume of the system. We use the mean value theorem on this term:

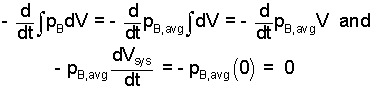
(7) 7

There is but one "shaft work" term and we know the work is "to the system." that is, positive."

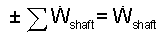
(8) 8

The term "extrinsic work rate" is non-zero for systems that accelerate or experience elevation change of the center of mass. Our system does neither. And there are no "special" work mechanisms (such as electric, surface or torsional) for this system.

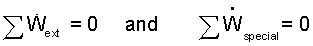
(9) 9

By these steps we reduce the energy equation from its general form (3) to the equation below which applies to our system.

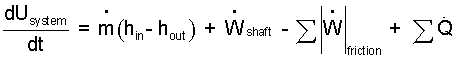
(10) 10

Drop the summations because there is only a single species and a single stream.
There is no "special" manner of work active, W_special.
dKE and dPE of the system are zero.
pe_in = 0 and pe_in =0.
ke_in = 0

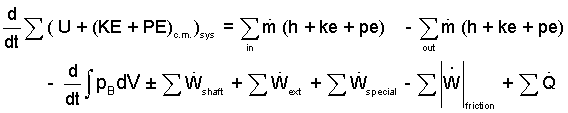
(11) 11

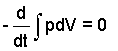
(12) 12

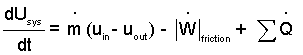
(13) 13

This inlet "construction" proceeds as follows (for simplicity - suppose the water to be flat and still):

imagine a very long fishing net. The net has floats along the top and weights along the bottom.
the net hangs in the water like a curtain.
the net is deployed in a great circle on the surface of the reservoir.
the net is somewhat strange since the vertical distance - floats above to weights below is only an inch or so.
the water enters the system moving along radial lines pointing toward the center of the circular area.
the perimeter of the circle is so large that the entering water velocity is essentially zero, hence ke_in = 0.
the surface of the water is designated at "zero elevation." Hence pe_in = 0, for the entering water.

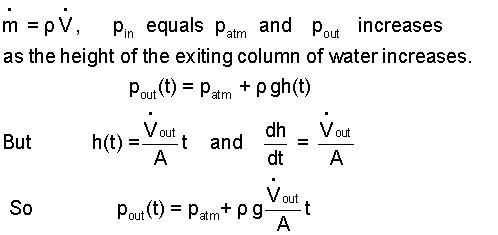
(14) 14

Now, this goes into the Energy Equation as follows:

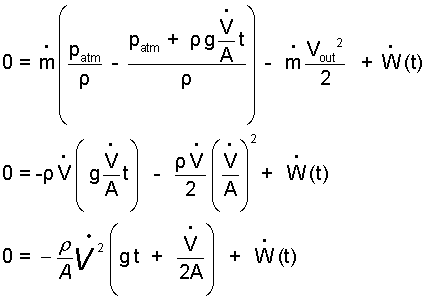(15) 15

Closed System Perspective To analyze the pumping from a closed perspective we divide the large mass of water into two parts. The larger part, II is essentially inactive. The mass equation for the system's two parts is:

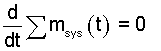(16)16

Obviously the level of II diminishes as water moves up the vertical pump. However, the vastness of II is such that the change of potential energy and kinetic energy of II is inconsequential.

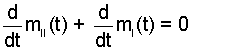(17)17

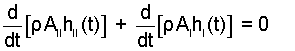
(18) 18

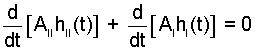
(19)19

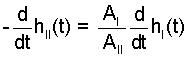(20) 20

This PE and KE belong to the "part I" water in time as it proceeds up the pipe. There is no water in the pipe initially. The speed the surface of the water moves upward equals dh(t)/dt which equals the volume rate of the pump divided by the pipe area. The center of mass is located at h(t)/2. The result of this analysis is the same as the previous open system analysis.