Extruded Rod

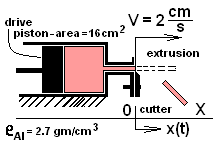
Aluminum exits from an extrusion die at constant speed of 2 centimeters per second and a cross-sectional area of 3 square centimeters. Once the extrusion is established, a cutter actuates regularly to chop the exiting aluminum in lengths that have a mass equal to 100 grams. The sketch shows the process at the instant (t = 0+) a section was cut. That is:

Calculate the time lapse between each cut.
♦ The constant speed, constant cross-sectional area and constant density of this problem make it easy to solve, almost without a plan. This solution deliberately takes a longer path to use and explain a powerful tool of calculus; Leibnitz differentiation. System selection is critical and all thinking and analysis thereafter must be system consistent. To get started on any problem, define a system. If that first choice runs aground, start over.

We take the system of one "extrude and cut" event to be is the length of mass extruded. The sketch to the right shows that mass at three times of its event. Inspected the figure from bottom to top. At t = 0+, an instant after the previous cut, the system mass equals zero. Above at an arbitrary time, t = t*, the length of the system mass equals X(t*) and finally (above again) at t = t_cut, a mass of 100 grams has been extruded, so it is cut. We write the system mass as an integral with a variable upper limit, X(t).

(1) 1

For our simple case, ρ and A being constant, we could just remove them from the integral and integrate it. But for the sake of learning, we pretend they are not constants. We rewrite the integral (with those terms as variables) then take the derivative of the system mass with respect to time.

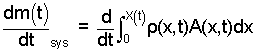
(2) 2

In the above equation, the term right of equality is the derivative with respect to time of an integral that has a function of time as its upper limit. We will use the classical approach to determine that derivative. Given a function G(x,t), to determine dG(x,t)/dt , form the difference, G(x, t + Δt) - G(x,t), divide the difference by Δt, then take the limit as Δt becomes zero. Our G(x, t) and the steps are:

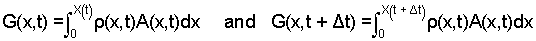
(3) 3

The difference is:

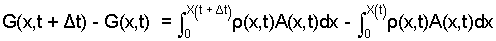
(4) 4

Next, to bring the integrals together, we interchange the limits of the second integral. Do you recall that Rule?

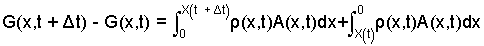
(5) 5

Above, we see the lower limit of the first integral equals the upper limit of the second. So those two integrals can be written as one:

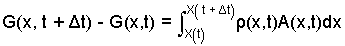
(6) 6

Keep in mind: we are ignoring that ρA is constant in order to deal with the integral in a general fashion. Our next step is to apply the Mean Value Theorem of Calculus to the integral above right of equality. The theorem format, with our use of it just below is:

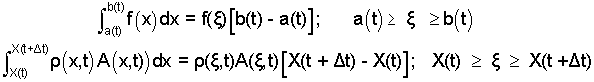
(7) 7

The function, f(x), varies over the limits, a(t) ≤ x ≤ b(t). The mean value of f(x) is f(ζ). Applied to our integral we obtain:

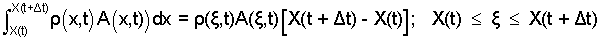
(8) 8

Thus the "difference" we are constructing becomes:

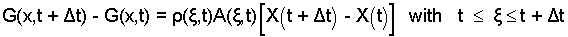
(9) 9

Next we divide by Δt and let Δt → 0. Left of equality we get dG(x,t)/dt immediately. We will explain the steps for "right of equality."

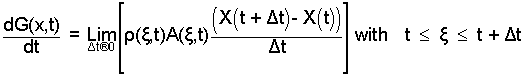
(10) 10

The density and area move ahead of the limit operation; they contain no Δt.

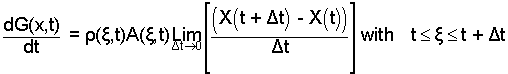
(11) 11

Look as the expression aboe right. Notice that as Δt vanishes, in the limit we have: t ≤ ζ ≤ t. Thus ζ is squeezed to become t.

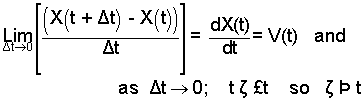
(12) 12

We obtain:

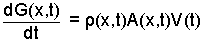
(13) 13

Below we replace G(x,t) with the integral it has represented.

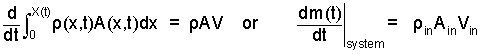
(14) 14

Above right is the usual first order differential equation. The subscripts "in" are appropriate. Our system is empty initially. As aluminum extrudes into space, our system "fills." Separate variables, integrate and put in the numbers.

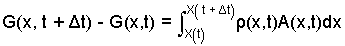
(15) 15

The numbers are unimportant. Our mathematics developed the mass equation with an "in" term. The mathematics can be manipulated easily to produce an "out" term. And there might be many "in" and "out" occurrences. An equation for that physics would be:

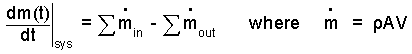
(16) 16

Calculate the speed of the drive piston. To proceed, a system must be selected. What system selection might tell the drive piston speed? A previous problem, FLOW THROUGH AN EXPANSION, can be used here. We apply that result to a system mass bounded by the moving face of the drive piston and a moving plane across the face of the exiting extrusion. The mass between those planes is constant.

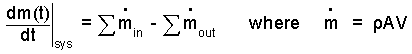
(17) 17