Freeze–Dried Rattlesnakes

The Bible says "snakes are evil." Consequently some people kill every snake they possibly can. One business sells dead snakes. A rattlesnake is suffocated and, while flexible, a stiff wire is shoved through its corpse, length-wise from rattles to fangs. The wire is bent to support the dead snake in a threatening "poised-to-strike," pose. Next the snake is frozen solid (-20°C) then placed inside a sealed chamber equipped with a vacuum pump. With prolonged pumping all of the air in the chamber then ( a great while later) all of the water in the snake's body are pumped out, leaving a preserved rattlesnake trophy.

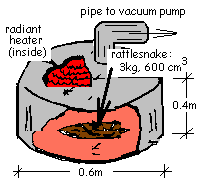
Radiant heating is used to expedite the process. All of this is made possible by the snake-catcher and thermodynamics. ^[1].

Freeze drying of the snakes commences once the chamber pressure attains 0.25 kPa. During pump-down, air is removed at the constant volumetric rate: V-dot = 1 x 10^-6 m³/min.

Calculate the least time required for the pump-down process. Note that this is just the first stage of snake treatment. The pump will need go much longer as the water diffuses out of the snake to "dry" it. We don't know how fast the water will leave the snake.

♦ The pump-down machine extracts air from the chamber and forces it into the surrounding atmosphere. The mass equation states the physical fact that the rate of change of mass within the chamber is equal to the rate at which mass is removed from it.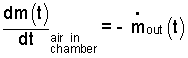

(1)

The mass equation with a
single exiting stream.

The term left-of-equality is derivative from classical mathematics as invented by Newton and Leibnitz.

Upon initiation of pump-down, the air inside is an ideal gas. As pumping proceeds, the air pressure will decrease. This assures the air will continue to obey the ideal gas law. The ideal gas equation for the system mass, with the system volume being constant is:

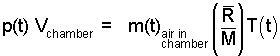
(2)

The "ideal gas" equation applies 
to the gas within the chamber.

Now we address the term right-of-equality. This term is not a derivative in a calculus sense. This term is physical; it depicts rate of mass passing through a section of system boundary. We seek m(t) so we rewrite our mass equation as:

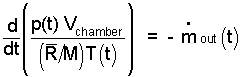
(3)

Enter the gas equation into the left
side of the mass equation, Eqn-1, then 
take the derivative to obtain Eqn-4.

The resulting equation includes the possibility that the temperature of air within the chamber might change as the pumping proceeds, that is temperature might be a, T = T(t). This will complicate matters. So we assume the pumping process is slow such that the remaining air can experience heat and maintain a constant temperature. The new mass equation is:

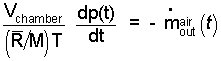
(4) 4

Now, by the equation, we see (by the term right-of-equality) that as air is "slowly" pumped from the space the pressure of air within the space decreases. Next write the mass rate of the mass expelled more explicitly. That is, m-dot, equals the instantaneous density of the system air times the volume rate of the pump, "V-dot".

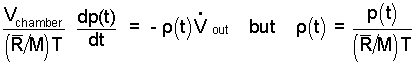
(5) 5

Next we substitute the ideal gas relation (above right) into the mass equation (above left). Please check the substitution and rearrangement - it should be:

(6) 6

We solve this first-order in the identical manner all of the previous equations. Separate variables, apply integration with proper limits and use integral calculus.

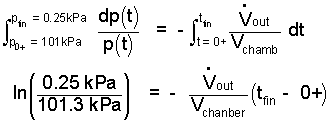
(7) 7

Remember to subtract the volume of the snakes from the chamber volume. Or should we?

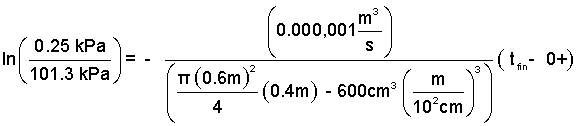
(8) 8

Proceed with the algebra.

(9) 9

Having an answer, we think about our assumption of constant temperature of the system air. It would seem the 4 hours would be slow enough that the air inside would stay at -20°C.

1 Freeze-Drying is more complicated than depicted above. We consider only the "removal of air" stage of freeze-drying. Actual prediction of process times requires knowledge of diffusion of water in snake flesh. At vacuum and frozen, the water molecules will migrate to the surface of the snake's body slowly then to become water vapor and be "pumped out."