| THERMO Spoken Here! ~ J. Pohl © | TOC NEXT ~ 221 |
Linear Valve
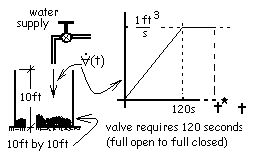
The supply of water to an empty tank is controlled by a valve which is initially closed. While opening the valve, the flow of water (into the tank) increases linearly. To open the valve completely requires two minutes and when the valve is "full-open" one cubic foot per second of water flows into the tank. The time required to close the valve completely is also two minutes.
Calculate the least time required to fill the tank and the overflow that will happen.
♦ To fill the tank in the least time, the valve is left full-open until the water level attains the top of the tank. Thereafter, while the valve is being shut, overflow will occur.
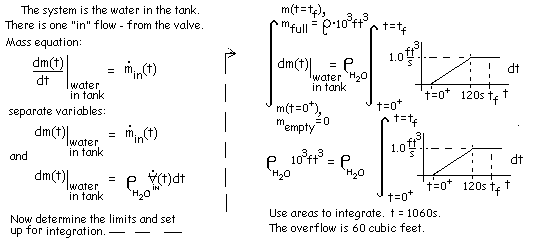 |
Calculate the least time to fill the tank with zero overflow.
♦ To prevent overflow one must have the valve "shut" the very moment the tank is full. Shutting the valve requires time. So we need to know at what time after the start (t = 0+) "closing" of the valve must commence?
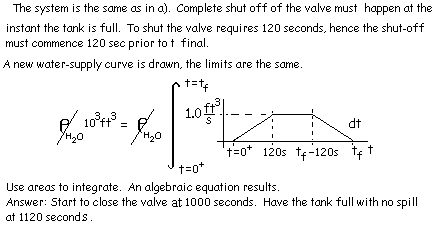 |
Linear Valve

The supply of water to an empty tank is controlled by a valve which is initially closed. While opening the valve, the flow of water into the tank increases linearly. To open the valve completely requires two minutes and when the valve is "full-open" one cubic foot per second of water flows into the tank. The time required to close the valve completely is also two minutes.
Calculate the least time required to fill the tank and the overflow that will happen.