| THERMO Spoken Here! ~ J. Pohl © | TOC NEXT ~ 217 |
5.01 Mass Equation
All engineering systems consist of matter the simplest property of which is mass. There is a general equation that "accounts" for system mass and all manners of its behavior (the system being correctly specified, of course). Logically we name that system equation after its property, the Mass Equation. The Mass Equation is an implicit, first order, differential equation with system mass as the dependent variable and time as the independent variable. This form is often called the rate-form. The equation has two types of terms, each potentially time dependent.
The position in the equation, left-of-equality, is reserved for system changes expressed as the derivative of the system mass. Generally this is one term, m(t) for a stationary mass. More terms might be needed when the mass boundary moves. Equation positions right-of-equality are reserved for "flux" or "transfer" terms which represent mass flow across the system boundary. The sign convention is "plus" for a mass flow which (in the absence of other effects) causes the mass of the system to increase (to become greater as time proceeds). Signs along with subscripts "in" and "out" are redundant but helpful.
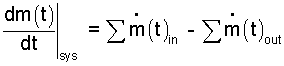
| (1)
The ”Mass Equation“ applies to every thermodynamic analysis. |
The mathematical form of the term left-of-equality, dm(t)/dt, is the typical derivative from calculus. Its variables can be separated; it can be integrated. However the form of terms right-of-equality is engineering math, not calculus. The units are the same (left and right) but right-side terms do not permit separation of variables.
The above equation represents the general idea of mass and space. Applications of the idea are complicated by "how the mass moves" and the spatial perspective selected. In its use the equation must be specialized to the physics of the case. And since the equation describes only "changes," an initial condition might be needed for a complete solution to be obtained.

| (2) Constant mass. |
For a system with constant mass but with "change-of-volume" expected we would write:
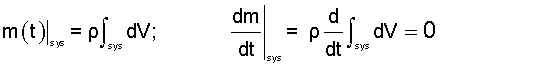
| (3)
Constant mass with constant density. |
If density is not constant the left term might be written as:
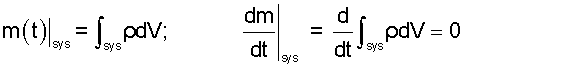
| (4)
Constant mass with variable density and space. |
The terms "right-of-equality," called mass flows, are instantaneous changes, as is dm(t)/dt (for the system), but these changes are not derivatives from calculus. Engineers often refer to the terms as being "m-dot" in nature where the dot denotes mass flow across a boundary. These terms can be expressed in terms of the density, flow velocity (a vector) and area of entrance (or exit) which is also a vector. In our cases (to start simply) it is assumed that the fluid velocity at all entrances and exits is directed perpendicular to the "area" at their mutual locations on system boundaries.
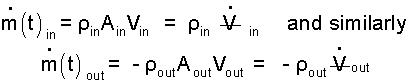
| (5)
Mass flux expressed in terms of local properties at the system boundary. |
Little remains to be said here. The examples that follow span the range of "typical" applications of the Mass Equation.