Block Slides on Ice

A block of copper (m = 1.6kg) rests upon a smooth plane of ice. Initially the temperatures of the copper, the surrounding atmosphere and the ice are 0°C. In an instant, motion is imparted to the block causing it to slide across the ice slab at an initial speed of 2.5 m/s. Also immediate, sliding friction acts to cause the speed of the block to decrease. Ultimately the block comes to rest, attains the speed, 0 m/s.

Calculate the greatest mass of ice (solid water @0°C) that is changed to water (liquid water @0°C) by the event.

System: It is ice and copper that interact. We take the system to be the copper and that ice initially solid which finally is liquid (at 0°).

Energy Equation: The physics is an "increment" event. Everything is 0°C to start, and everything is "vast" so we assume all stays 0°C; hence there will be no heat. (also a "prompt" event promotes the assumption: no heat.

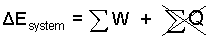
(1)No HEAT. Everything is vast and at 0°C

The "system" is two parts. We expand "energy" to identify its parts as "copper" and "water."

(2)The system is copper (assumed solid initially and finally)
and water (assumed solid initially and liquid finally).

The easiest next step is the identify the ΔE's as internal energy and kinetic energy changes.

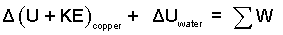
(3) Energy equation of the event.

A bit of thinking is involved. Both copper and water are "simple compressible" substances. The work term, ΣW, expands but it does not have a "friction" term because that effect is interior to the copper/ice event. Pressure is constant at 1 atm, the work of copper and water are as shown below.

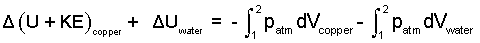
(4) For the event copper and water have
"work" in their "pdV" forms.

We take two steps to proceed. First we integrate the two integrals immediately right-of-equality to get their "Δ" forms.

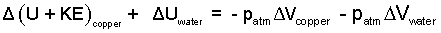
(5) (5)

Next we move those "work" pieces left-of-equality to right-of-equality, collect them and use the fact, "h = u + pv ".

(6) (6)

Apply the numbers.

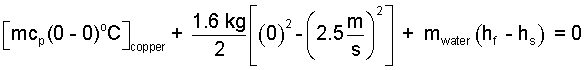
(7)(7)

Put the given numbers into the above. But in reality, were one to slide a copper block as depicted, would there be a small trail of liquid water left. Might one gather that water and measure its mass? No. It is unlikely that air and ice might be at precisely 0°C.

Another thought is that the copper block might simply have been dropped from a height to have the 2.5 m/s speed upon impact. The same solution as above would apply.

Copper Block Slides on Ice

A block of copper (m = 1.6 kg) rests upon a smooth plane of ice. Initially the temperatures of the copper, the surrounding atmosphere and the ice are 0°C. In an instant motion is imparted to the block causing it to slide across the ice slab at 2.5 m/s. Immediately sliding-friction causes the speed of the block to diminished; ultimately the block attains the speed, 0 m/s.

Calculate the greatest mass of ice (solid water @0°C) that is changed water (liquid water @0°C) by the event.