THERMO Spoken Here! ~ J. Pohl ©

TOC NEXT ~ 134

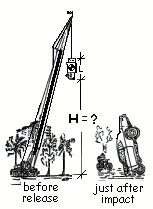
Drunk Driving Awareness

At a Health Festival the Sheriff's Association showed teens the horrific damage of a head-on auto collision at 70mph (~ 1.6 km/hr). A crane hoisted a junk car (mass = 1000kg) to a height sufficient, upon drop, for the car speed to be 70 miles per hour then impact solid concrete ground. The event is quite convincing.

I. Required Elevation: Calculate the height the crane must raise the car above ground, "H".
♦ As our system we take the car, a short length of crane cable and Earth. The car is an extended BODY of length, "L" with center of mass located at "L/2." The energy equation in increment form is:

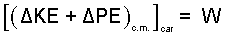
(1) 1

To determine the needed elevation, we imagine dropping of the car to occur. Write Eqn-1 explicitly. For the drop, the speed initially, V₁ is zero and the c.m. elevation is H + L/2. As the car falls, there will be work of drag, the resistance in falling through air; this work is not zero but small. Our equation becomes:

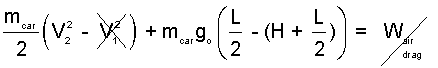
(2) 2

Eqn-2 reduces (below). Solution for the height is at hand, Eqn-3.

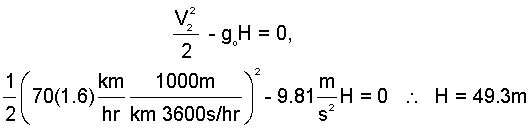
(3) 3

II. Least Work to Lift To crane cable does work to lift the junk. Calculate that work.
♦ The work of an event can be made quantitative by calculation using the (i) Energy Equation of the system event or evaluation of the lifting (ii) Force-Displacement Integral. These calculations correspond to the left column and right column of the table below, respectively:

(i) Energy Equation	(ii) Force-Displacement Integration

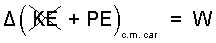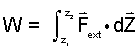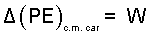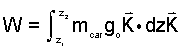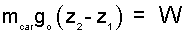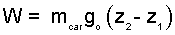The above calculations provide only a "lower limit" of the work event. The work could be much greater for an accelerated or jerky-type ascent. Also this limit could never be realized due to friction and the necessary accelerattion (however small) needed.

vvvvvvvvv

(5) 5

vvvvvvvvv

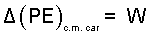
(6) 6

vvvvvvvvv

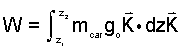
(7) 7

vvvvvvvvv

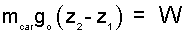
(8) 8

With work there is movement of the system and with movement there is friction. Knowing that friction opposes the movement, we write it's work component with a negative sign (-W1-2, friction). Part of the work causes energy change of the system. Some call this the "useful" work.

The energy change of the car is its kinetic energy and or its potential energy. The energy equation is:

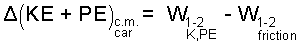
(3)

Next, we write the energy equation with changes in terms of the event property changes. The initial speed |V| is zero and so also is the final speed. Notice that the first elevation is set as simply z1 and the second elevation as z1 + H. It is likely that friction will be small. Our energy equation becomes:

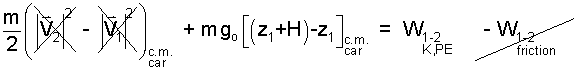
(4)

The energy equation (above left) is solved for the work.

(5) No need to algebraically rearrange this equation.

Calculate the least height the hulk must be raised such that 70 mph is attained at impact with the ground?
♦ Take the car as the system, modeled as an extended body. We write the extrinsic energy equation with a "friction work" term included.

There is no extrinsic work (marked as X), the only surface force acting is drag which belongs to friction work. Friction or the drag force at seventy miles per hour is not inconsequential, but we approximate (until later study) by assuming friction work is negligible (marked as /).

The kinetic energy change is a matter of speeds; the initial speed is zero miles per hour and the final speed is 70 mph. For the potential energy change, we assume the car center of mass located midway in its length (L). The potential energy change is as written:

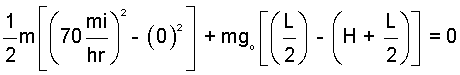
(3) 3

The mass of the car divides from the above equation. The implication is that the mass of the car has no physical effect or influence on the event. This is obviously not true. Our assumptions have distorted reality.

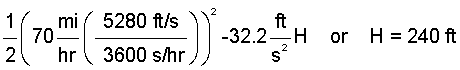
(4) 4

The "approximated" event is called "mechanical equilibration." Initially the hulk was held above Earth (in a state of constrained equilibrium) by the crane. Once released the car moved to a second state of constrained equilibrium - on the concrete. Mechanical equilibration events are common. In "Water Seeks its Level," water is constrained by a valve, then released to flowed to a new constrained state. (Check the Index ~ heat is mentioned there also).

Perform an analysis of the car for an event that ends ten seconds after release.
♦ The kinetic energies are initially and finally zero ( X ). We assume friction, as before, is small ( / ). The loud crash heard is a small amount of extrinsic work arriving to our ears ( / ) . The smash of impact involved a very great force at the front of the car but since the hulk did not move into the concrete, there was no work. We write the energy equation with dropped terms:

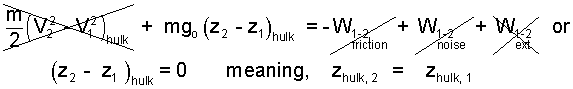
(5) 5

So we arrive at the absurd conclusion that the car was not dropped. The explanation is that the car, in fact, is not an extended body but a collection of particles and as such has internal energy. An energy equation suited for this event must include internal energy. For the fall and bounce to rest, the new equation predicts a change of hulk internal energy.

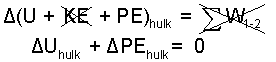
(6) 6

Were you to put your hand on the hulk (where it is likely to get bent the most) before it was lifted and after, you would feel that the metal was warmer. That indicates increased internal energy. Internal energy change equals mass times specific heat times temperature difference. The above equation can be written:

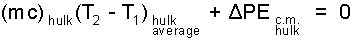
(7) 7

Finally, define the event to have a two-hour duration. The equation above is the result for an event lasting "ten seconds." But were you to wait two hours before putting your hand (a temperature measuring device) on the car, you would find its temperature equal to what it was before the lift, T₁. This means the internal energy had returned to "what it was." We write T_2,average equals T_1,average in the above equation.

(8) 8

So the equation tells us again that the car was dropped through "zero" distance. There is a natural companion term to internal energy: heat. The Extrinsic Energy Equation (adjusted again) becomes:

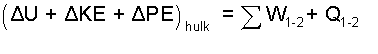
(9) 9

The physicality of dropping this car caused us to introduce internal energy and heat informally. It is logical to add these terms to the Extrinsic Energy Equation.

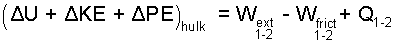
(10)10

Let's look at the event again:

Release and Fall to 70 mph: The second speed was prescribed to be 70 mph. Initially the car temperature war equal to ambient temperature. Physically (for now) internal energy change of the car relates to temperature change and or its destructive deformation. meaning the potential energy of the car (relative to this datum) by the fall has become zero. But that potential energy is now (but for friction) kinetic energy of the car. The car is millimeters away from the concrete.

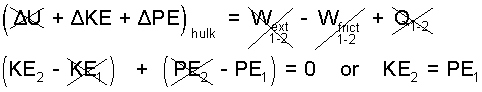
(11)11

Release to crash, bounce then rest: This perspective adds the catastrophic smash to the previous event. The initial and final velocities are zero. The car is so large, its temperature increase will be difficult to notice. There is too little time for there to be heat. This event is, in effect, a conversion of the kinetic energy into internal energy of the car. The energy equation reduction is as follows.

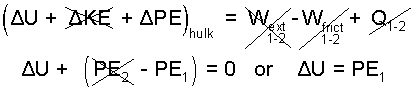
(12) 12

Release to crash till two hours later. The internal energy of the car is related to its temperature, which just after the crash, was greater (on average) than the surrounding ambient temperature. Give time, heat would occur, the car temperature would return to ambient temperature and the internal energy would be equal to its original value.

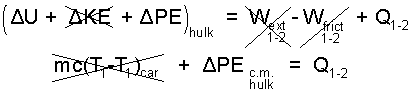
(13) (13)

Thermodynamics is a convoluted topic. There comes a time when the student rebels against further assumptions and approximations. Internal energy and heat, which were needed for this discussion are not new ideas. Internal energy will be addressed more formally soon. It is illogical to ignore the temperature increase with this event and the subsequent heat of the system. Heat is difficult to make quantitative.