THERMO Spoken Here! ~ J. Pohl ©

TOC     NEXT    ~   129

Boy in a Wheelchair

This problem arrived at Physics Help Forum some time ago. The problem poses some difficulties. This is a discussion of those aspects.

Problems of texts are contrived. To illustrate a physical principle an educator creates a physical premise for a mass and its event. Dimensions are given and perhaps a sketch. The words describe a physical event Finally a question or answer is asked.

The problem statement implies a physical mass/event obeys some conservation principle which is represented by a mathematical equation (or equations) that contains a number of terms. The author "gives" (states as known) some of the equation terms. When this "given" (or known) information is sufficient for calculation of all terms of the equations except one, the problem is said to be "well-posed." That last term is "requested," it is the "answer" to be determined regarding the mass and its event. The previous is a description of what is called a "well-posed" problem.

The problem of this discussion (written above in italics) is special as follows.
i) Generally, "given" information of a problem is something knowable before the event or some fact that might be physically set at the start. To know the "average friction force" for an event is unusual.
ii) The matter of a basic problem is a single molecular species. Here we have a "boy" and his "wheelchair." Compound systems can be difficult - let us see.
iii) The boy is a biological entity. Only for specially crafted problems will the laws of physics or thermodynamics apply to living persons.

Solution and Discussion: Despite reservations, solution will be attempted.
♦ System: A system must be selected. Taken individually we might choose the "boy," or the "chair." Or we might choose to analyze the "boy and chair" taken together. As a rule, the larger, more encompasing system one might use turns out to be easiest to solve. Thus, as system, we select: boy and chair."

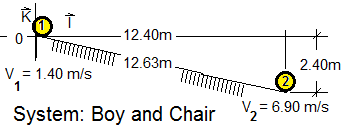♦ Sketch: A sketch showing dimensions and the event information is helpful. Our coordinate space will be "0XZ."

♦ Analysis: "Average friction force" being mentioned, Newton's Second Law might apply. But the query request is "work of the boy." Work is a term of an energy equation.

The energy equation is writen, Eqn-1. System components are "boy" and "chair," hence system energy is written as two terms, Eqn-2.

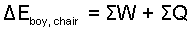
(1) (1)

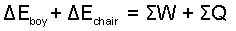
(2) (2)

♦ About Heat: In basic thermodyamics heat is either: i) "given", ii) the unknown sought, or iii) heat is zero. We assume prior to commencement of the roll-down event that the system was in thermal equilibrium. Heat requires temperature difference and time. Although al­tered temperatures might happen in roll-down, we assume there to be insufficient time for heat. Hence we set ΣQ = 0 in Eqn-3, below.

Eqn-3 presents the energy components as increments: internal, kinetic and potential. Also the work is divided into that of friction (drag) and "other."

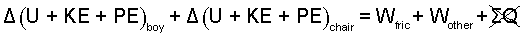
(3) (3)

Procede left to right with Eqn-3. Write the internal energy change of the boy first, separately. Next, the specific kinetic energies and potential energy of the boy equals that of the chair so group and subscript as "both." Internal energy of the chair might change with a change of its of temperature or volume but neither change happens: the chair internal energy is constant. Eqn-4.

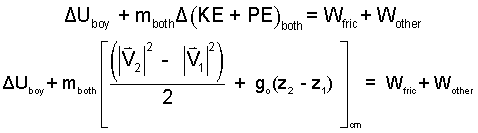
(4) (4)

It makes sense to insert some of the numbers we are confidant about. These steps are shown as Eqn-5. In the result of Eqn-5, work of the chair is struck out. The chair is simple compressible, dW = -pdV. For the event there is no dV.

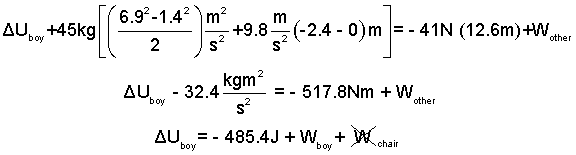
(5) (5)

This final equation form has internal energy change of the boy left of equality. This might be about zero provided the boy is motionless. However, if ΔU_boy is zero then W_boy is positive meaning energy as work entered the boy. This is complicated as are most systems having a living component.

Boy in Wheelchair

Knowing geometry and having observed eclipses of the moon, Eratosthanes came to believed Earth was a sphere. To measure its circumference, he devised a plan to used the rays of light form the sun. He assumed all rays from the sun arrived at Earth parallel, each to all others.

Premise presently unwritted!