| THERMO Spoken Here! ~ J. Pohl © | TOC NEXT ~ 120 |
Harpy's Nest
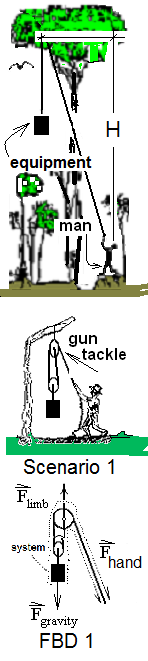
To observe Harpy Eagles nesting, a naturalist built a blind in a neighboring tree. A line attached to a crossbow arrow was shot through the tree canopy. Next a hook is attached to a stout limb. Finally, by climbing pulley, equipment then the observer are hoisted "H" meters into the tree.
Two types of lift effected by the man are the Equipment Lift and the Self-Lift. For each type calculate:
(i) the least force applied by the man,
(ii) the least length of rope hauled, and
(iii) the least work of the man.
= = = = = = = = = = = =
Note: The man might apply a large force, haul quickly and accelerate the load. Thereafter he might pull slowly. Each manner-of-lifting-effort would have a different associated force for and work for the same actual accomplishment. Our considerations of "equipment-rope-pulley-man" events will treat only slow-frictionless lifts. Such events are called "quasi-static," "quasi-equilibrium" or "reversible."
Equipment Lift:
Scenario 1 depicts this lift.
(i) Least Force Required: For a very slow, frictionless, "quasi-static" pull of the man, we apply Newton's 2nd Law with the system as the equipment, rope, and tackle: the free body sketch is FBD-1. For the "quasi-equilibrium" lift, the rate of change of momentum is "vanishingly small," so set "left-of-equality" equal to zero. The gravity force of the equipment is mequipgo.

|
(1) |
Can this be solved? No! Write as components to see.
In Eqn-1, the force subscripted "limb" and and that subscripted "pull" cannot be determined. When "unsolvable" is encountered, selection of a "smaller" sub-system of the first system might be a remedy. As sub-system of FBD-1 we choose, simply the lower pulley, FBD-2.
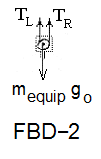 The boundary of the sub-system, FBD-2, cuts through three ropes of the lower pulley. We assume pulleys to spool without friction. Hence the rope tensions in the upward lengths (on opposite sides of the roller) are equal, TL = TR. A sum of moments about the pulley center will show this. Conclusions for FBD-2 are:
The boundary of the sub-system, FBD-2, cuts through three ropes of the lower pulley. We assume pulleys to spool without friction. Hence the rope tensions in the upward lengths (on opposite sides of the roller) are equal, TL = TR. A sum of moments about the pulley center will show this. Conclusions for FBD-2 are:
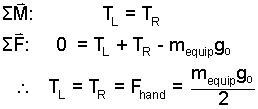
| (2)4 |
Eqns-2 conclude each supporting line tension to equal mequipgo/2. By analysis of the upper (assumed frictionless) pulley we determine the pulling force: Fpull = 300N.
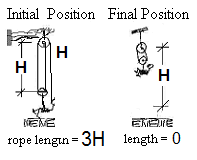
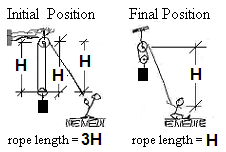 ii) Least Length of Rope Hauled:
ii) Least Length of Rope Hauled:
The sketchs (right) (showing "initial" and "final" configurations of the pulley system) make it clear that the man must haul "2H" meters of rope.
(iii) Least Work of the Man:
The least work of this event can be determined by integration of the work definition Eqn-3.
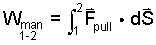
| (3)
Integration of the force-displacement scalar product. |
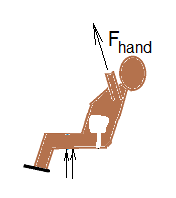
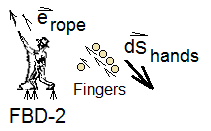 We know |Fpull| is constant and we know the length of the pull, Lpull. To understand clearly how the integration must proceed, a new free-boody-diagram (somewhat hard to draw) is needed. FBD-2. shows the man supported by Earth. His hands are wrapped arfound the rope;the small detail shows that the force acting on his fiungers acts upward. The motive of the rope is to lift the man.
We know |Fpull| is constant and we know the length of the pull, Lpull. To understand clearly how the integration must proceed, a new free-boody-diagram (somewhat hard to draw) is needed. FBD-2. shows the man supported by Earth. His hands are wrapped arfound the rope;the small detail shows that the force acting on his fiungers acts upward. The motive of the rope is to lift the man.
For calculations a unit vector is defined as erope. This unit vector is always aligned with the rope and directed upward. A differential displacement of the mans hands is written: dshands, (part of the surroundings) applies force to the boundary of the system with one hand and pulls it (the rope) downward. His other hand then grasps the rope above and pulls it down. With effort he displaces consequitive parts of the system boundary downward, grabs a next section of boundary, and so on.
For the incremental pulling events, we define the direction the rope moves to be a unit vector parallel to the rope. Imagine the vector to be just above the man's grip, parallel to the rope, and directed toward his hands. Call that unit vector, erope. With this unit vector, we can write the force applied to the boundary of the rope and the displacement of the rope as needed by the work integral and then integrate it. The force of the man is: Fpull. The differential displacement of the force is dS. Work as the integral of force through displacement for the event is written:
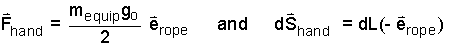
| (5) 5 |
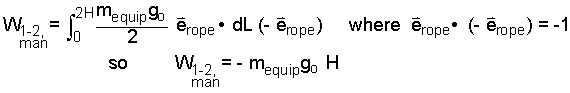
| (6) 6 |
= = = = = = = = = = = =
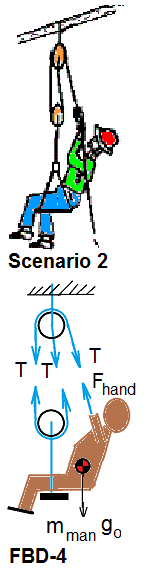 Second Lift: This lift is an effort whereby the man straps himself into the harness then hand-over-hand hauls himself upward. The sketch (right) shows the configuration of ropes and the man for that event. The gravity force acting is mmango.
Second Lift: This lift is an effort whereby the man straps himself into the harness then hand-over-hand hauls himself upward. The sketch (right) shows the configuration of ropes and the man for that event. The gravity force acting is mmango.
(i) Calculate the force required of the man and the length of rope he must haul.
 In a manner similar to the hoist of the woman, we see the force must be 300 Newtons and that 90 meters of rope must be hauled.
In a manner similar to the hoist of the woman, we see the force must be 300 Newtons and that 90 meters of rope must be hauled.
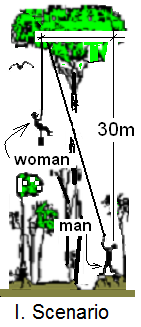
Harpy's Nest
To observe nesting eagles, naturalists built a blind. With a cross-bow, a line was passed through the canopy of a neighboring tree. Next a block and tackle (a "gun tackle" shown below) was hoisted and manipulated to attach to a secure limb.
First Lift: The woman got into the harness and the man hauled rope to lift her (mg = 500 N) to the tree top. Calculate the work by integration of hauling force applied to the rope times its displacement. Next calculate the same work by use of the energy equation.
Premise presently unwritted!