THERMO Spoken Here! ~ J. Pohl ©

TOC     NEXT    ~   121

BUOY LIFT II

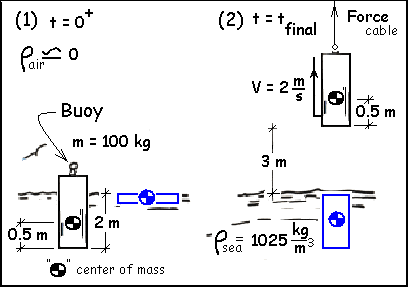
The sketch, (1), shows a buoy floating in the sea. A cable lowered from a dock is attached to the buoy and the buoy is hauled to state (2). Take the system to be the buoy, a short length of the cable and part of the sea.

Calculate  the least work of the cable.
♦  The system will be the buoy and "that part" of the sea that is involved. "That part" is sea water initially on the surface which resides finally (once the buoy is lifted) in the space occupied by the buoy initially. The schematic shows the sea water and its center of mass in blue. This is a "batch" event which initiates from complete equilibrium, experiences work and attains state (2). The energy equation has two energy components: the buoy and that sea involved. The energy equation in increment form is:

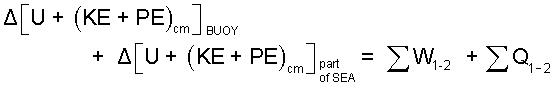
(1) 1

In beginning thermodynamics heat, (ΣQ) is the easiest term of the energy equation to address. Upon initiation of the event (at t = 0-), the sum of heats to the buoy and sea (ΣQ) equal zero because the buoy and sea are in thermal equilibrium with the atmosphere. There is no expectation that this "lifting" event will cause any significant temperature change anywhere and hence create no motive for heat. The approximation that Σ Q ≈ 0, is a reasonable simplification of this problem.

Next, the internal energy of the buoy and the internal of energy of the sea water are functions of temperature and specific volume. U = U( T,V ). For the event we expect no change of temperature or volume for the buoy. There will be a small local temperature change for the sea water ~ we assume that number to be negligibly small. Thus ΔU_buoy≈ 0 and ΔU_{sea water}≈ 0 are reasonable simplifications. The energy equation becomes:

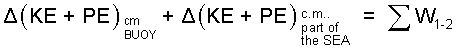
(2) 2

Now specify the kinetic and potential energy changes and insert the numerical information from the schematic. This problem was worked before as BUOY LIFT I. From this current vantage only one work component, work of the cable, is relevant.

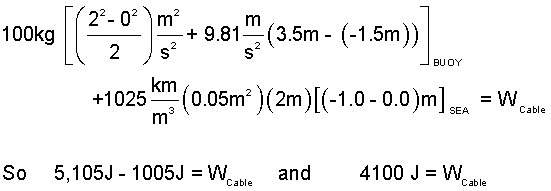
(3) 3

Why is this work not the actual number but the LEAST possible work.
♦  With the event, there will be splashing and swirling of the water. The event imparts energy to the water and that energy dissipates into the surrounding water. Our calculation ignored that face - the number for work calculated in a minimum value.

Buoy Lift II

The sketch, (1) shows a buoy floating in the sea. A cable lowered from a dock is attached to the buoy and the buoy is hauled to state (2). Take the system to be the buoy, a short length of the cable and part of the sea. The cable moves the buoy for condition (1) to condition (2) as shown.

Calculate  the least work required of the cable.

Premise presently unwritted!