Density of Fluid "A?"

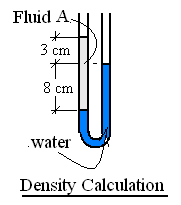The glass U-shaped tube contains 11 centimeters of "Fluid A" (in the left leg) above water.
Calculate the density of fluid A.

♦ Since the fluids are static, the hydrostatic equation applies. As a first task in applying the hydrostatic equation, one searches for physical scenario to find a place where the pressure is known. Sometimes there is no place where the pressure is known explicitly. In those cases there is usually a place where the pressure can be reasonably assumed. In this problem, the place is the the water surface on the right side; there the pressure is assumed atmospheric. We write the hydrostatic path from there downward through the bend then upward through both fluids to arrive at the surface of Fluid A (in the left leg).

p_atm + ρ_waterg_o (0.08m) - ρ_Ag_o(0.13 m) = p_atm.

The "principle" was applied above. So go ahead and do algebra to it!

ρ_A = (8/13)ρ_water = (8/13) 62.4 lbm/ft³

Therefore we determine the density to be: ρ_A = 38.4 lbm/ft³.

Density of Fluid "A"

The glass U-shaped tube contains Fluid "A" and water. Since the fluids are static, the hydrostatic equation applies.

Calculate the density of fluid A.