| THERMO Spoken Here! ~ J. Pohl © | TOC NEXT ~ 50 |
GOD Lifted Earth II
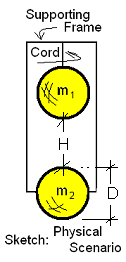
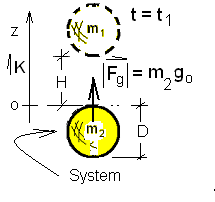
Often, to understand an event, one must reduce the situation to a simpler model. The sketch to the right is a "physical scenario" similar to the system of the previous example, "GOD Lifted Earth I." Our sketch shows two spheres of equal mass held in a state of constrained equilibrium by a rigid frame and a cord. We assume these are the only masses that exist and that the surface gravity of each is represented by go. The cord represents the catalyst.
Event: The event begins when the cord is cut. We set that time to be t = t1. Also, when the cord is cut the rigid frame is stripped away. We see this condition (below left) with no forces shown because no system has been selected. Logically, we wonder, "What happens?"
Analysis requires that a system be chosen. We choose the system to be Mass "1,", m1. The next step, according to Newton, is to "isolate" the system schematically and ascribe too it whatever forces might apply. In choosing a system (below center), all else of the physical situation (below left) becomes surroundings (below right).
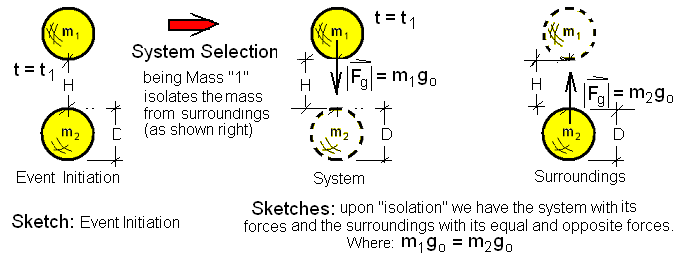
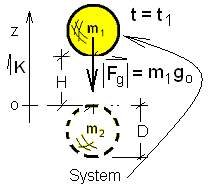
At this point, having Mass "1" as the system, we can specify spatial coordinates then apply Newton's Law of Motion to that mass - "1."
 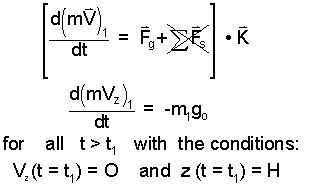
| (1) 1 |
Free Fall of Mass "1": The above sketch of system with coordinates, governing differential equation and initial conditions constitutes what is called a consistent set or statement for solution of the event. That solution states that the mass, beginning with zero velocity a distance H from Mass "2," moves with increasing speed toward Mass "2." While this solution might be effected now, let us first consider the other mass, Mass "2."
The system might just as well been chosen to be Mass "2." The equations would be as shown below.
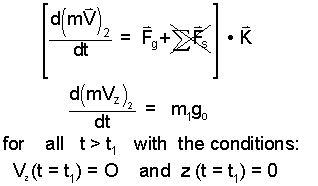 |
(2) 2 |
Free Fall of Mass "2": A feature of this physical system, that is quite difficult to put into words, is that it is symmetric. Once the cord is cut and the frame deployed, we expect mass "2" to move also. Mass "1" will move downward and mass "2" will move upward. Due to symmetry, we intuitively deduce that the spheres will contact at the z-coordinate, H/2.
The statements of, "Free Fall of Mass 1" and of "Free Fall of Mass 2" simply initiate the solution. Before we proceed recognize that with Mass "1" as system, Mass "2" is its surroundings and for Mass "2" as system, Mass "1" is its surroundings. For either system there is a force "on the system" and on its respective surroundings, an "equal and opposite force" applies. When a system and its surroundings are combined the system perspective ceases to exist and the "equal and opposite" force-pair sum to zero. That is, combine the system and surroundings (either mass as system) yields the sketch, "Event Initiation." Expanding on this idea:
It is true that for every force there is an equal and opposite force. This means that all forces are pairs and that each pair sums to zero; hence there are no forces. But much is made of forces in physics and mechanics. How can this be?
The answer is subtle. Newton isolated the system from surroundings. While the system and surroundings were together, many "force-pairs" acted. But upon "isolating" of the system from the surroundings one force of the pair acted on the system, the other on the surroundings."
Continuing with the event of Mass "1" (as system). We know that impact of the two will occur. To solve for "where contact occurs" normally requires simultaneous solution for Mass "1" and Mass "2." In our (purposefully simplified) case we know by virtue of symmetry that contact will occur at the location to be H/2. (Note: were the masses not equal, we would have to use the condition "zero distance between the spheres" or "distance of fall of "1" plus distance of rise of Mass "2" equal to H.

GOD Lifted Earth II
Often, to understand an event, it is convenient to construct a simpler model to solve. The sketch to the right is a 'physical scenario" similar to the previous example, "GOD Lifted Earth I." Our sketch shows two spheres of equal mass held in a state of constrained equilibrium by a rigid frame and cord. We assume these are the only masses and that the surface gravity of each is represented by go. Think of the cord as a catalyst. When it is cut, an event will occur.
Premise presently unwritted!