| THERMO Spoken Here! ~ J. Pohl © | TOC NEXT ~ 36 |

Scenario shows person holding pota- toes. To the right is a FBD in which the ambient density of air is assumed equal to zero.
Ten Pounds of Potatoes
The English Engineering System (~1824) mass was set to be a dimension and defined as a certain quantity of matter. Balances and other means of extension of quantification of mass were built. The "founding mass" was a cube of metal kept in a vault in France with replicas for distribution. Force was a less certain aspect of reality. In Newton's 2nd Law, force was (and is, largely) written "left-of-equality." This gives the impression (if not in fact, the intent that force is defined by the 2nd Law, i.e. by the equation:
In those times "force" was an idea more subtle than mass. One immediate idea of force was the "effort" required by someone to support a mass in his hand. Some clever lads supposed force to be a dimension as is mass. Going further, they gave quantification to force. They defined a "unit force" (one pound force) to equal in magnitude, "that force" required to support a unit mass (one pound mass) at sea level.
Thus to support or carry ten pounds mass of potatoes (in uniform motion) a person must exert a vertical force of ten pounds force. When we apply Newton's 2nd Law to the event of uniform motion (in the vertical direction, 0 = ΣF) a necessary identity among units (for potatoes and everything) results.
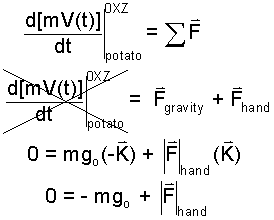
| (1)
Newton's 2nd Law: d(mV)/dt = ΣF |
English Engineering defines the magnitude of force required to support an object at sea level to equal the magnitude of mass of the object. Atwood measured the gravitational acceleration. Put these numbers into the result - Eqn-1.
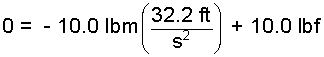
| (2) (2) |
This equation seems peculiar because all quantities are known. What the equation reveals is: "Engineers who chose mass, length, time, and force as independent dimensions, then ascribe their units arbitrarily, will discover: i) the dimensions are not independent and ii) their units are related by a constant of proportion. In the case of the English Engineering System, this constant (to sufficient accuracy for our purposes) is 32.2
Equation (2) yields the fact that in the English Engineering System (where F, m, L and t are defined) the relationship among units is Eqn-3 (left). In contrast, the metric system defined only mass, length and time as dimensions. Units specified are the kilogram, meter and second. Force is left to be a "derived" entity. Were metric units used in the above consideration we would obtain Eqn-3(right).
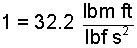
| (3) (3) |
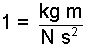
| (4) (4) |
More About English Engineering Units
When the English Engineering System was formulated the common usage of Newton's 2nd Law was F = mA. Units were given to dimensions but the four dimensions are intertwined in Newton's Second Law of Motion. Not long thereafter the overspecification became apparent as Eqn-3.
Discovery of the fact, Eqn-3, caused something of a stir. Some gave this equivalence a special name, "gravitational constant" notated as: gc, Eqn-5. The new constant was inserted into F = mA, Eqn-6. Others seeing that gc was in fact "1" thought it strange to give "1" a name.
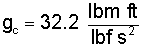
| (5) (5) |
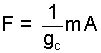
| (6) (6) |
Some in the scientific community wanted not the constant, 32.2, to not show up at all. One idea was to alter the mass unit to be the slug (1 slug = 32.2lbm). Or the force might be changed to the unit, poundal. Enough said!
Physics has adopted System Internaionale Units. This has reduced confusion. To reduce confusion is always a good idea. A further clarification would be to not use the equation, "F = mA," infavor of Newton's form - Eqn-7.
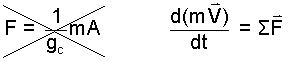
| (7) (7) |

Scenario shows person holding pota- toes. To the right is a FBD in which the ambient density of air is assumed equal to zero.
Ten Pounds of Potatoes
When English Engineering units were specified (~1824) mass was set to be a dimension and defined as a certain, specific quantity of matter. The "founding mass" was a cube of metal kept in a vault in France with replicas for distribution. In those times "force" was an idea more subtle than mass. One immediate idea of force was the "effort" required by someone to hold or support some mass in his hand. Some clever lads supposed force to be a dimension as is mass. Going further, they gave quantification to force. They defined a "unit force" (one pound force) to equal in magnitude, "that force" required to support a unit mass (one pound mass) at sea level.
Premise presently unwritted!