Hand Supports a Mass

The standard acceleration of gravity (at sea level and 45° latitude) is 9.80665 m/s². At that location
a) Calculate the force is required of a hand to support at rest a mass of 2 kilograms.
b) Calculate the mass a force of one Newton could support.

Effects of the ever-present atmospheric air are often negligibly small. We assume ρ_air ~ 0.

♦ Our system is some mass of 2 kilograms that is supported by a person's hand. The image (above right) is a scenario of this event.

To apply Newton's Second Law of Motion requires a "system schematic." The mass must be isolated and the forces shown. See the free body diagram below right. Sonntag assumes, without statement, that no effect of atmospheric pressure is involved. 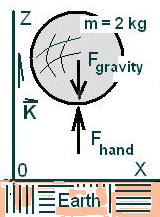A system sketch (FBD) of the scenario mass
modeled as a BODY. The density of ambient
air is assumed negligible.

The forces are those of gravity and the hand. Newton's Second Law for the mass with these two forces is:

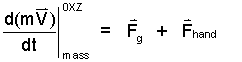
(1) 1

The velocity of the mass is zero. Only vertical forces act so we scalar multiply Newton's equation by K.

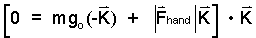
(2) 2

Next we use the fact, K • K = 1. We enter the surface acceleration and solve for the magnitude of the force:

(3)

♦ The next part asks the mass that a force of 1.0 Newton could support. We use the equation (2) from above:

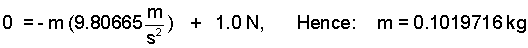
(4) 4

This problem is from Sonntag. It is misleading and a waste of time to carry such precision. A device that could measure a force to the precision of 19.61330 Newtons or a device that could measure a mass of 0.1019716 kilograms would cost millions of pounds.