Civil War Memorial

Many statues have been erected in honor of the soldiers who died in the Civil War. A typical monument (this one in Mulberry, Tennessee) is shown. Suppose you were to observe the original and to notice that it was at rest.

Model the statue as a BODY. What does Newton's Second Law of Motion tell us?
♦ The first step in application of the Second Law is to identify and isolate the system. In this case we sketch the statue "extracted from reality" and represented as a system (typically called a free body diagram). We represent it as a body with a center of mass and forces as indicated. We assume the time to be t = 0+ and (by observation) that the initial values of position and velocity of the BODY are observed and known.

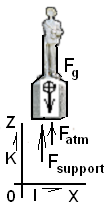
The above statements of physical fact are called "initial conditions." Next we write the Momentum Equation for a BODY (this is Newton's Second Law of Motion:

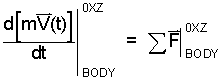
(1)1

Although we are dealing with a First Law of Motion situation, the Second Law works as well - with zero velocity the Second Law reduces to the first. For zero velocity, momentum is constant therefore the Second Law of Motion becomes two statements. The table shows these:

Newton's First Law of Motion can be considered a special case of his Second Law which written with notation for a BODY is two equivalent equations:

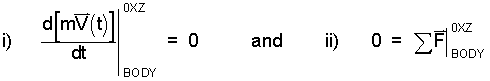
(2)2

Solution is the mathematical task of integration of the differential equation. This procedure is said to be "classical" which means "at the very basis of mathematics." The first order differential equation is very common. You will see this same procedure executed again and again in your studies. The steps even have names!

Separate Variables As written above, the left side of the differential equation has two variables. The differential of momentum, d[mV(t)] is called the dependent variable. Time, t, is the independent variable. Upon multiplication of this simple equation by dt, the variables become separated:

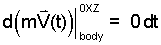
(3)3

Integrate the Equation First apply integration symbols to both sides of the separated equation:

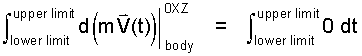
(4) 4

Two integrals are obtained. To proceed, each integration requires specification of its "lower limit" and "upper limit." When dealing with equations, a good approach is to do the easy parts first. The integration of time is easier. Knowing the event initiates at a definite starting time; the right side lower limit is set as: t = 0+. The upper limit in time would be either an "ending time" or as in this case just some later time. The upper limit is written t = t.

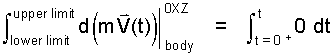
(5)5

To specify the left-side limits, correspond them to the already stated, right-side limits. For the lower limit the body momentum, mV₀₊, (corresponding to time, t = 0+), is zero because the velocity is zero, mV. Since the upper limit of integration of time is indefinite; so also the left-side upper limit integration of momentum must be indefinite.

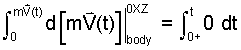
(6) 6

The limits now in place, we integrate.

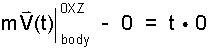
(7) 7

Interpret the Results: The conclusion of our mathematics states:

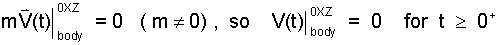
(8) 8

Thus the velocity of the body was zero at t = 0+, and remained zero for all times thereafter.

We can take this a step further.

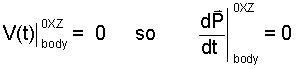
(9) 9

Above right we have another first order differential equation which requires an initial condition of position to be solved. Obviously the body was somewhere at t = 0+ . That place is P(t = 0+). So we repeat the process:

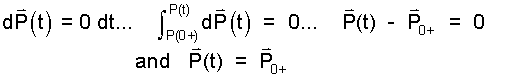
(10) 10

This last statement says for all times (including t = 0+) the position of the body is "where it was."

This first solution of Newton's differential equation is trivial in that the answer was known before we started. Nonetheless we solved its first order differential equation. Behaviors of very many physical systems can be expressed mathematically as first order differential equations. Solution steps are classical. So return... reread and confirm that these ideas of space, time frame, initial condition and such are correct. Commit this solution to memory; be able to reproduce it on a bar napkin to impress your date!