Valentino's Wake

From 1920 through 1934, Rudolph Valentino, starred as a dashing hero in over a hundred silent screen movies. But in 1936, at the peak of his popularity, he died. His body was displayed at his wake in an open casket. One newspaper asserted:

"Today 9,000 persons per hour passed Valentino's
casket in solemn tribute."

Is it possible that 9,000 people could have walked past his casket in an hour?

♦ While it cannot be determined if this happened, it can be determined if this did not happen. A newspaper photo showed there were four lines of viewers. With reasonable assumptions, we can determine, approximately, how many persons might have walked past the coffin in an hour.

The line will move with uniform motion. Our system will be a person, that very last person in line who moves uniformly and will be the last person to view Valentino in one hour hence. We label the person "Last." The position of that last mourner, at the start and for all times within the hour is:

P_Last(t) = P_{Last, 0+} + V_Lastt

(1)

Check this Equation at the time: t = 0+.

Walking in procession, we estimate each mourner would move about 1.5 feet per second toward the casket. Also lets assume the line of mourners extending from the last to the person beside the casket (at any instant) is straight. This is unlikely. The line is apt to wind down streets and around corners for blocks. We use an "X" coordinate with the unit vector directed from the last person toward the casket (see sketch). To assume a straight line will not disqualify our calculation.

P_Last(t) = P_{Last, 0+} + (1.5 ft/s I)t

(2)
The people move in the positive “I” direction.

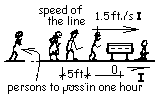
When peaceful mourners walk in a line, they maintain space between themselves. We estimate each person would occupy about five feet of space, five feet of length (on average) of the procession line. Thus the position of our "Last" person in line at the start (the beginning time of our observation, at t = 0⁺) would be 5ft N feet away from the casket, where the letter "N" represents the number of persons ahead of our "last" person at any instant.

P_{Last, t =0+} = 5ft N - I

(3) At 0+ the Last person is located in the negative I direction.

Use the above fact to update the first equation.

P_Last(t) = - 5ft N I + (1.5 ft/s I) t

(4) 4

This is a good place to explain the meaning of "time equals zero, (t = 0)" and "time equals zero plus, (t = 0+)." Both times are the same time. Zero means zero and the "plus" means a very, very short time later. The purpose of the distinction is to emphasize the beginning nature of an event. When, if ever was time zero. Yet we use the idea "time equals zero" to designate beginning. A close word is epoch. Our usage is: t = 0 before an event (nothing happening) and the event commences at t = 0⁺. Both times are zero, one with nothing happening, no clock running, the other start-time is part of the time of the physical event.

In an hour, according to our uniform motion model, our mourner named "Last" will be beside the casket, that is standing at the origin (position zero) with time equal to one hour (t = 0+ + 3600s). We apply these numbers:

0 = 5ft N(- I) + (1.5 ft/s I) (3600s/hr)(1 hr) or so, N = 1080

(5)
5

But the photograph showed four lines of mourners. Thus, by our estimate, a maximum of (4 x 1080) 4320 mourners could pass the casket. Our assumptions are reasonable; we conclude the reported number, 9000, is wrong.