Ladder-Boom Rescue

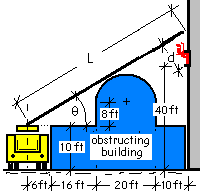
Imagine a retirement home is ablaze and flames have backed two elderly women to the opening of a rear, third story window. A ladder truck has arrived in a back alley but a building obstructs its reach.

To place the ladder at the window, it will be extended nearly vertical to the correct, laser determined, length L, then tipped downward to the angle θ. Lasers will obtain the dimensions (given in the sketch) and a computer will solve the geometry. To provide a test case, use the information of the sketch.

Calculate the length of the length, "L," and its angle of elevation, "θ."
♦ A first step is to label points on an initial sketch. At point A, the ladder touches the obstructing roof. Point B is at the center of the dome of that semi-circular (20ft dia) roof. Once programmed, laser controls of the truck can deal with the geometry.

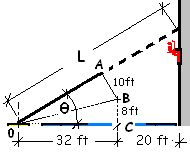
Angle θ equals the sum of two angles:

θ = angle C0B + angle BOA.

By trigonometry of its triangle, angle C0B is determined in two steps:

0B = (32² + 8 ²)^1/2 = 33.0 ft

sin(C0B) = 8 / 33, hence angle C0B is 14.0°

Similarly, angle B0A is 17.6° and θ = 14.0° + 17.6° = 31.7°

What length of boom is required for the rescue?
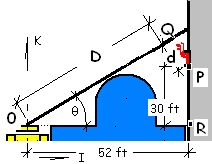♦ The distance from the base of the ladder to the wall is 52ft, so the length of the ladder is:

L cos( θ) = 52 ft or

L = 52 ft / cos(31.7°) = 61.1 ft.

First we write an implicit vector to the point P (where the women are at the bottom of the window) then we equate this to a second implicit vector to P.

0R + RP = 0Q + QP

We make these vectors as "explicit" as possible (distances are in in feet):

52 I + 30 K = 61.1 e_0Q + d e_QP

By inspection of the geometry, the unit vector e_0Q can be written in terms of theta as:

e_0Q = cos(31.7°) I + sin(31.7°) K.

Enter this information into the equation:

52 I + 30 K = 61.1[cos(31.7°) I + sin(31.7°) K ] + d e_QP

Our next task is to obtain an explicit form for e_QP, which is perpendicular to e_0Q. In fact, at the point P, there are two unit vectors perpendicular to e_0Q. We write them promptly as:

e₁ = sin(31.7°)I - cos(31.7°)K and

e₂ = - sin(31.7°)I + cos(31.7°) K

These vectors are written directly from e_0Q by swapping the component magnitudes and changing one sign. That e_0Q is perpendicular to 1) and 2) is easily proved by the conditions of perpendicularity:

e_0Q • e₁ = 0 and e_0Q • e₁ = 0

We seek e_PQ which has a positive I component and a negative K component. When we enter this result into our equation we see that it has two unknowns which are d and D.

52 I + 30 K = D [ cos(31.7°)I + sin(31.7°) K ] + d[ sin(31.7°) I - cos(31.7°) K ]

Collect on I and K to obtain:

I: 52 = D cos(31.7°) + d sin(31.7°)

K: 30 = D sin(31.7°) - d cos(31.7°)

To solve these equations, multiply the first by sin(31.7°) and the second by ( -cos(31.7°)).

52 sin(31.7°) = D cos(31.7°) sin(31.7°) + d sin²(31.7°)

- 30 cos(31.7°) = - D cos(31.7°) sin(31.7°) + d cos²(31.7°)

Now add the equations:

52 cos(31.7°) - 30 sin(31.7°) = d [cos²(31.7°) + sin²(31.7°)]

d = [52 sin(31.7°) - 30 cos(31.7°)]ft. = 1.8ft

Which is close enough for a successful rescue!

Sensors built into the truck components will provide status data of the system, the operator will select a desired second position of the boom end. Nearly instantly computer output to movement mechanisms will direct motion of the machine. In setting up this system one is obliged to do an initial, complete calculation, then rearrange the solution to have logic flow. A sound method must be established; computers can't program themselves.