Prove: (A - B)² = A² - 2AB + B²

The Greeks understood the totality of anything
to always equal the sum of its parts.

We begin with the slightly easier task; a proof regarding (A + B) ². (This proof was made by Euclid around 300 B.C.)

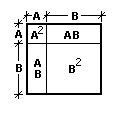
By inspection of the figure to the right, it is apparent (add the areas).

(A + B)² = A² + 2 AB + B²

But we need (A - B)². So Let's use the identical square areas but assign new lengths for the previous A and B such that (A - B) arises as a factor. The second sketch, below right, shows these choices.

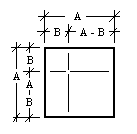
Again the area of the outer square will equal the sum of its areas interior:

A² = (A - B)² + 2(A - B)B + B²

A² = (A - B)² + 2AB - 2B² + B²

Now, rearrange and collect the above equation to obtain:

(A - B)² = A² - 2AB + B²   Q.E.D.

A technique used in geometry is also used in thermodynamics. Break things apart, solve, then put the pieces back together.

Prove: (A - B) ² = A ² - 2AB + B ²

The Greeks understood the totality of anything
to equal the sum of its parts.

An easy way to precede is to begin by with a slightly easier task regarding ( A + B )². The common result was first obtained by Euclid around 300 B.C.

Premise presently unwritten!