Microwave Coffee

A cup of day-old coffee (25°C, 500 cc) was put into a microwave oven and "heated." After a minute and fifteen seconds, the oven bell rang and the coffee was removed. Its temperature was measured to be 90°C.

Calculate the least electric work the water received from the microwave?
♦ This is an increment-type event. The energy equation is written as:

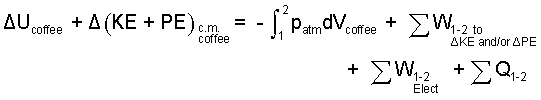(1) 1

There will be no change of kinetic or potential energy of the liquid coffee. (nor work associated with such), (X).

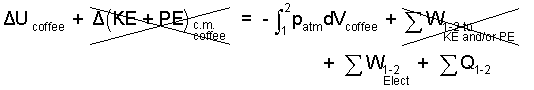(2) 2

By definition, heat is energy transfer from matter at high temperature to matter at a lower temperature. Microwaves become inconsequentially hot as they are used. Energy transfer of the microwave to the water occurs through radar or what might be called frictional electric work - not heat.

There is heat from the steaming water to the cooler interior of the microwave. That heat is counter-productive. The "least energy" from the microwave corresponds to ΣQ = 0.

In addition, since there is only the microwave, we drop the summation, Σ from the electric work term. Also, this being a constant pressure event, we combine the compression work with ΔU to become ΔH.

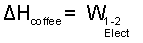(3) 3

The enthalpy difference is written as:

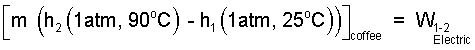(4) 4

The above form is suited for retrieval of data from a table. We proceed to Table 4.2.2. The advantage of tabular data is accuracy. The disadvantage is that the information is discrete and interpolation is required. The interpolations are done below. The values entered into the equation.

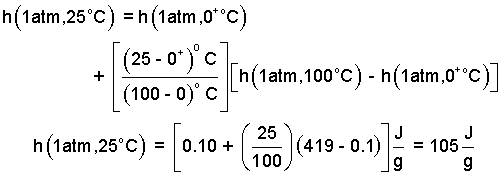
(5) 5

One more interpolation yields:

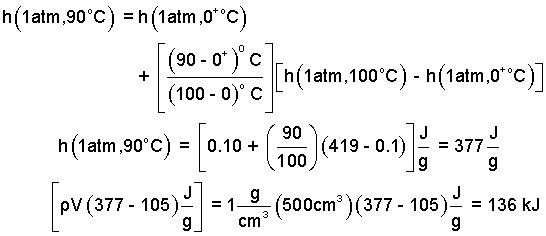
(6) 6

To use an average specific heat approach, we restate the above as:

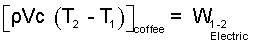
(7) 7

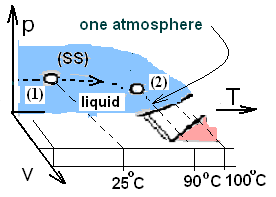
The sketch, above right, shows the path of change of the water in state space. Our water is initially liquid (1 atm, 25°C) and finally liquid (1 atm, 90°C). We obtain the specific heat from the table (Column 3 - Row 3):

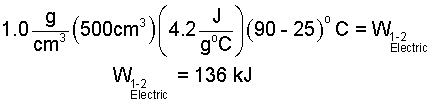
(8) 8

What average power does the water experience?
♦ The work, expressed as the integral of a work rate over the event time is:

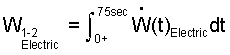
(9) 9

This cannot be integrated as is. We apply the Mean Value Theorem to obtain:

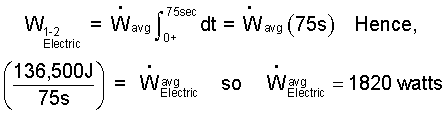
(10) 10

It is emphasized that the above calculations are actual accomplishments of the microwave; energy that indeed arrived to the water. As for the machine, how much of the power from the household electric network it squandered, we don't know.