3.19 Energy Equation: SUBSTANCE II

Our goal is a complete, competent Energy Equation. So far we have the simplest external (extrinsic) energy equation in which energy changes and work relate directly to the displacement of the body (system).

That equation is inadequate for systems other than those realistically modeled as a body or extended body. Our energy equation must be extended to include energy changes and work consequent to system deformation (as well as displacement). The new energy we need is internal energy. This new type of work, is intrinsic and is called compression work. The energy of any substance is changed by compressive forces that diminish their volumes.

The table shows a hierarchy of energy types and work, ideas introduced in HS physics and how they evolve to be used in the first two chapters of a thermodynamics text. Nomenclature and notation will always bedevil thermo students. There is no lingua franca of thermodynamics educators. Hopefully the table will be helpful, hopefully.

Results are presented in accord with SYSTEM TYPE:

BODY: as system (including the EXTENDED BODY).

Energy Types	Work Expression
Kinetic and Potential (mass, elevation and speed) i) (KE + PE)_c.m.	Body Displacement (force and displacement) ii) ΣW_ext
EXTRINSIC ENERGY EQUATION
Δ(KE + PE)_c.m. = Σ W_ext
(i) Kinetic energy and potential energy are first associated with the center of mass of the body. The body, point mass or extended body does not have rotational kinetic energy. (ii)Extrinsic work involves displacement.

Energy Equation and Terms for a Substance
SYSTEM	ENERGY	WORK
INTRINSIC (a compressed gas)	Internal (temperature and specific volume) U	Intrinsic (pressure and volume change, and ~~modes~~) iii) -∫p_BdV + ΣW_modes
INTRINSIC ENERGY EQUATION	iv) ΔU = - ∫p_BdV + ΣW_modes + ΣQ
ENERGY EQUATION	ΔU +Δ(KE + PE)_c.m. = -∫p_BdV + ΣW_ext + ΣW_modes + ΣQ
Kinetic energy and potential energy are first associated with the center of mass of the body. The body, point mass or extended body does not have rotational kinetic energy. Extrinsic work involves displacement All substances have the intrinsic work mode, "compression work:" ( -∫p_BdV) Other work modes are but slightly discussed here: (ΣW_modes). Heat is added to make things "come out even." Some say this equation is the definition of heat.

This section introduces the idea "intrinsic" as something belonging, collectively, to a collection of particles. Not something about a single mass but about millions of particles, a continuum. Intrinsic work is an involved topic while internal energy is less so.

Internal Energy To suppose the energy of a fluid (composed of a billions of small bodies, its molecules) could be written as a sum of the individual potential and kinetic energies of each of the billions of particles seems logical. Were that massive task successful, the energy of the gas would be expressed:

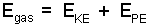(1) ♦ ...

Properties of the kinetic energy portion of the gas energy would be average molecular mass, m_i and the speed , v_i of the individual kinetic energy of the googol of gas particles implied by the equation:

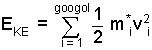(2) ♦ ...

While none of the information required to pursue this path can be known, all is not lost. Some of the energy it represents can be made quantitative, made measurable "in the whole" by definition of the "center of mass." The position of the center of mass can often be measures and so also can its velocity. This means the bulk, overall kinetic energy and potential energy can be quantified. With the basis, center of mass, the particle (i) positions are written:

P_i(t) = P(t)_c.m.,gas + P_i/c.m.(t)

(3) ♦ ...

When particle velocity (the derivative of position) is substituted in to the expression for kinetic The collective gas kinetic energy is divided into three pieces. Two, a linear kinetic energy and a rotational kinetic energy of the mass with respect to the center of mass of gas being measurable parts of the collective energy. The third term, the sum of the particle kinetic energies relative to the center of mass, is not measurable. . This term is the kinetic component of internal energy of the gas, U_{gas, KE}.

() ♦ ...

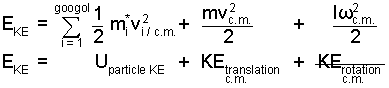Kinetic energy has a rotational part which is relevant with many systems. We have placed a strike-through on those terms not because they are zero but because this writing will not consider that aspect of energy. In a similar but more abstract manner gas particle potential energies can be divided into extrinsic, "center of mass," and internal components. In conclusion the energy of a gas is written.

() ♦ ...

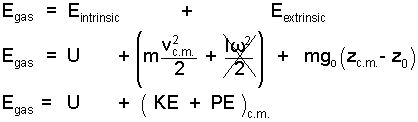What has been argued for a gas applies as well for a liquid or solid. Internal energy and intrinsic energy, synonymous ideas, are easier to understand than the energy change mechanisms, intrinsic work.

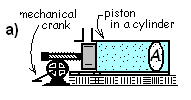gear COMPRESSION WORK: Compression work is introduced with the contained gas is our system. By action of the mechanical crank and gear, the piston is advanced into the cylinder. With compression of the gas, it is obvious there is work but the apparatus is arranged so the gas experiences zero event-wise extrinsic energy changes or extrinsic work. We assume no leakage of gas and no friction of the piston or gas.

Sketch b) depicts conditions of the gas and piston, after the crank has pushed the piston slightly (and slowly) to the right, an incremental distance ΔX. 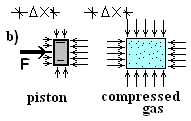. The energy, as work, is applied to the piston, passes through the piston. Our interest is the energy and work of the contained gas. First we consider the piston to make the argument that energy passed through it. Work arrived to the piston via the crank and gear; that applied force moved the piston in the direction of its displacement. The work was positive. The initial and final velocity of the piston are zero. Also, the piston center of mass moved horizontally, hence the potential energy change is zero. Modeled as an extended body, the piston extrinsic energy equation is (and tells us):

(ΔKE + ΔPE)_piston = ΣW
0 = ΣW

() ♦ ...

Since the piston is rigid, the work effect would have been an increase of energy of the piston. But there was no increase of piston energy. The energy transfer as work to the piston (at its left face) transferred from the piston to the gas (at its right face). We conclude energy as work passed "through the frictionless piston" to the gas. For the horizontal movement of the gas, the initial and final velocity of its center of mass was zero and the elevation of its center of mass did not change, hence ΔKE_gas = 0 and ΔPE_gas = 0. Yet energy transferred to increase the energy of the gas - its internal energy. An energy equation for the gas will have the form:

ΔU = W_{gas, 1-2}

() ♦ ...

In keeping with work as being a force times a displacement, with respect to the gas, the force would be the pressure-force (pressure of the gas times piston area), p_gasA. This force acts through the displacement dX seems unrelated to the gas until force and displacement as set side by side. For the gas the work would be:

() ♦ ...

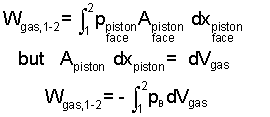Above, we recognized that A_pistondx_piston equals dV_gas, the differential change of volume of the gas. With this equation it is important to realize the pressure, the last integrand, is the pressure of the gas, "at the piston face," the moving boundary of the gas. To be remindful, this pressure is notated: p_B. During an actual gas compression (or expansion) pressure varies throughout the gas. Only upon the assumption "frictionless" is pressure uniform at p throughout. Practically always we set p_B equal to p but for understanding, this should be a conscious act. A final consideration is if the energy of a gas must increases (positive work) as its volume decreases, a negative sign is need be placed before our integral. The energy equation for compression (or expansion) work is:

() ♦ ...

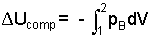Compression Work is called a "work mode" of all substances. The internal energy of all substances can be changed by compression work. There are other work modes. Oxygen, for example, responds work-wise to magnetic force. Sensors of automotive fuel systems measure that work effect and use it in their designs. Work done in extending or compressing a steel springs increases its internal energy.

HEAT:

The term in the last row of out table (extreme bottom, right) is ΣQ, which represent the sum of heats of the incremental system event. Heat happens when (and where) there is a temperature difference between a part of the system and a part of the surroundings. Every thermodynamic system, at time t = 0+ is assumed to be "in thermal equilibrium with the surroundings", meaning that the sum of system heats: ΣQ = 0 at the time,t = 0+.

With work events it is common for the substances to experiences a temperature increases, to become hotter than the temperature of the surroundings. Given time, system temperature and system energy associated with that temperature, will decrease as the temperature equilibrates with the surroundings. Energy transfer as a consequence of temperature difference is called heat. The sign convention is: in the absence of all other effects, that heat which causes an increase of energy of the system is positive.

Heat is difficult to predict and even in the best controlled laboratory circumstances hard to measure. The energy equation, as we write it, includes a "last" term written, ΣQ, which means the summation of all possible heat of the system. Thermodynamics texts deal with heat 0ΣQ by use of one of three stratagems:

♦ Heat is the UNKNOWN: Let the event heat be calculated. Apply all other information of the event so the energy equation has but one unknown: ΣQ.

♦ Heat is SPECIFIED: A second way to avoid heat is to specify that it is known (was controlled and applied precisely) for the event. When "precise heat" is stated, that number is entered into the event equations. Some other term is calculated.

♦ Heat is ZERO: The adjective, adiabatic, means no heat. Heat requires time. Thus heat being zero is a reasonable assumption (stipulation)for system events known to be quick or very fast. Slow events might be "argued" to be adiabatic by the stipulation that they are "perfectly" insulated. Perfect insulation does not exist.