WORK to Draw the Castle Bridge

The scenario shows a typical castle drawbridge used to provide access (when down) or deny access to the entrance (when up).

What least work is required to raise the span?
♦ Our system is the simple span of a drawbridge. To "select the bridge as system," is to isolate it (mentally). To do this, let your mind's eye trace the entirety of boundary of bridge. The event for the bridge will be that the "drawing ropes" pull it from a horizontal to vertical position.

For most of the bridge there is contact only with air. Two complications occur at the draw ropes and the bridge hinges. We simply pass a cutting plane through the ropes. A tensile force will act there. We imagine the hinges as two pieces with one part belonging to our system. We assume the hinge to be frictionless. A force will act on the system at the halves of the hinges.

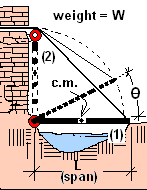
We assume the bridge hinge to be well-oiled- frictionless. The lowered position is defined as State (1). The position, full-raised to the vertical, is designated as State (2). Lift of the span occurs by forces of lifting ropes that act at the boundary of the bridge and are displaced. Forces also act at the bridge hinge but these forces do not displace.

What least work is required to raise the span?
♦ The system is the material of the span to be lifted. This is all of the wood, nails and such of the span. The span pivots at its hinge. Lifting ropes act at the end of the draw. Our system includes the bridge, the parts of the hinge that move and a short length "lifting ropes." The system cuts through the lifting ropes; the tensile, lifting forces act there. Assume our span rigid and uniformly distributed, model it as an extended body with its entire mass located at its geometric center designated, c.m., on the figure. As always, we write our tool, the energy equation. Then we use it to inspect the event.

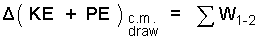(1) 1

"Least work," is a theoretical idea, associated with the "idea" of doing things very slowly. "zero velocity" is implied meaning the event does not happen BUT the least work can be calculated. So we raise this bridge so slowly that there is inconsequential change of kinetic energy and with vanishingly small velocities there is no wind drag. Only potential energy changes.

Regarding work, our system boundary cuts through the draw ropes at the right end of the bridge. The tensile forces applied throughout the ropes times their displacement will pivot the bridge from the angle θ = 0 to θ = 90° (the vertical position). At the castle side of the draw the system boundary is between the parts of the pivot hinge. We assume no friction of the hinge of the bridge. Our extrinsic energy equation with expanded terms is:

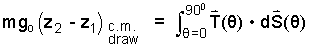(2) 2

Above, right of equality, is expressed the work of our event in a "force through displacement" form: ∫ F • dX. This term could be calculated DIRECTLY. To do so one would write an expression for the integrand of the vector integral, the tension of the ropes, as a function of angle of lift, T(θ). Next one would write an expression for the vector differential, "displacement of the end of the bridge, dS(θ)." Placing both expressions in the integral, one effects the dot product, then integrates to have the result. Direct calculation of extrinsic work can be tedious.

We write the work term more implicitly than ∫ F • dX;
we write it as W_1-2.

Fortunately, the potential energy change of the bridge is in the energy equation (left of equality). To calculate that is an indirect way of calculating the work. We use that approach with the definition of the bridge weight, W = mg_o.

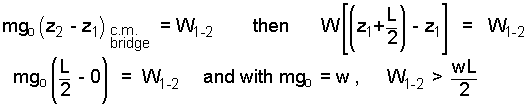(3) 3

The use of energy change (left-of-equality) to determine work is convenient. Our answer is the least work required. Put otherwise, if your greatest capability for work is less than the calculated number - you will not raise the bridge.

The following calculation, though a bit advanced, belongs here because it shows the effort required to perform the an integration of work. It is done clearly.

Determine the work by Integration. The vector diagram (below right) has notation required for these calculations. As an integration, the work is:

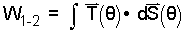(4) 4

The tension in the rope T(θ) and the differential displacement vary as the bridge moves from θ = 0 to θ = π/2;. We write this tension as a magnitude times a unit direction.

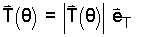(5) 5

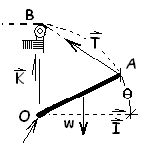
We calculate the unit direction first. The sketch to the right is needed. We recognize that e_T, unit vector direction of T is equal to e_AB. We write a vector equation that contains AB, then find its unit vector.

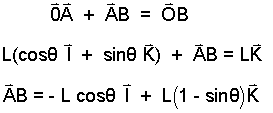(6) 6

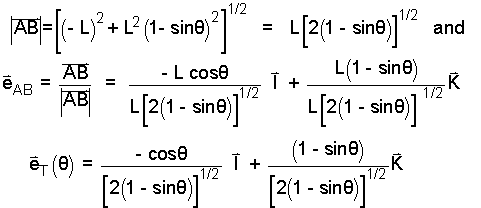(7) 7

To determine the magnitude of the rope tension, |T(θ)|, we sum moments about the bridge hinge.

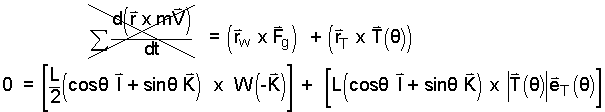(8) 8

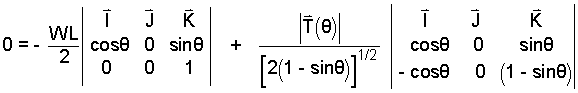(9) 9

Be careful of signs while performing the multiplication:

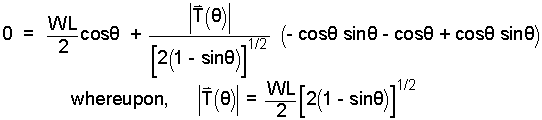(10) 10

Next we need the differential displacement, dS(θ). The magnitude of a differential displacement on a circle equals Ldθ. The direction of that displacement is the unit vector perpendicular to 0A with a negative I component and a positive K component.

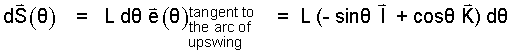(11) 11

We are now ready to put the pieces together. We seek this integration.

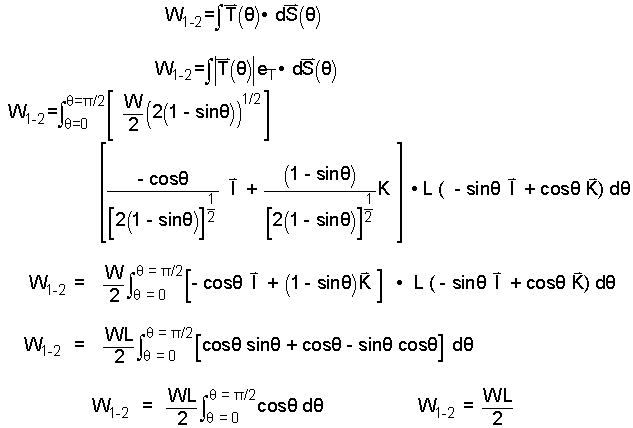(12) 12

Calculation of work directly is certainly a load compared to calculation by way of change of potential energy.

WORK to Draw the Castle Bridge

Work to Raise the Castle Bridge