| THERMO Spoken Here! ~ J. Pohl © | TOC NEXT ~ 59 |
Kinematics of Bar AB
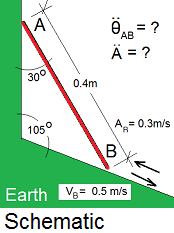 Typical text-book "given-information" sketch.
"Bar AB and Ground" constitute a kinematic mechanism. Connections at A and B (not shown) maintain sliding contact with the ground. At the instant shown, End-B has a velocity of 0.5m/s and an acceleration of 0.3m/s² (in the directions shown). Calculate the angular acceleration of the Bar-AB and the acceleration of End-A.
Typical text-book "given-information" sketch.
"Bar AB and Ground" constitute a kinematic mechanism. Connections at A and B (not shown) maintain sliding contact with the ground. At the instant shown, End-B has a velocity of 0.5m/s and an acceleration of 0.3m/s² (in the directions shown). Calculate the angular acceleration of the Bar-AB and the acceleration of End-A.
Note: There are many types of mechanisms and special ways to solve them. Here, the "answer" is of less interest than the method of solution which which is general and applies to all mechanisms.
♦ Setup: Vectors are used. Vector descriptions of a mechanism begin in general and are made more specific thereafter. The Position Triangle is our first step. We place the origin at the 105° angle. Just a general or "implicit" statement is needed to start. See the sketch, (below left). The Position Equation is written just below the sketch.
 Some beginning notations are needed.
Some beginning notations are needed.
| (1) |
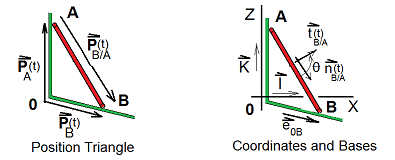
Position Triangle
The Position Equation reads as, "The position of "A" (which changes in time) plus the position of "B relative to A" (which changes in time) equals the position of "B" (which changes in time). Eqn-1 tells the geometry in a compact way. That the equation terms are vectors and time dependent; we know by the "over-arrow" of each term and the notation "(t)," respectively. The form of Eqn-1 is said to be "implicit."
To use Eqn-1 it must be written explicitly. This requires definition of coordinate references with unit vector bases. As you read below, refer to the sketch Coordinates and Bases.
1) We define a 2-D Cartesian reference attached to ground, origin at "0" with axes X and Z (this is an0XZ-space). Associated unit vectors are I and K.
2) Next imagine a pair of unit vectors scribed onto Bar-AB.
i) A normal unit vector, nB/A(t), on the line from A to B, points in the
direction of B.
ii) A tangent unit vector, tB/A(t) perpendicular to the normal.
iii) An angle of rotation is added to defined positive angle, angle rate and angle acceleration.
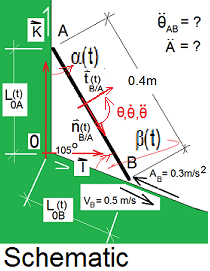 Full notation on a "too small" sketch.
Full notation on a "too small" sketch.
As tools of vector analysis are added, the schematic becomes a bit cluttered. With experience the transformed schematic will look as shown (right). The notation permits our vector triangle (Eqn-1) to be written more specifically.
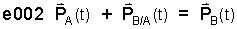
| (2) |
Implicit form of the Position Triangle.
Position Triangle: We use the defined lengths and unit vectors to rewrite Eqn-1 in a general manner.
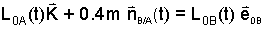
| (3) |
... making (2) more explicit.
Eqns-2 and 3 apply for address continuing time, that being what "(t)" means. This equation can be differentiated or one might "freeze" the equation by letting "(t)" be come "(t*)".
Position Specialization at t = t*: Eqn-3 can be used to calculate information at the special time notated as " t* ". The notation is to place an asteric, * , with the variable. Lengths associated with the instant, t*, are notated: L*0A and L*0B. Also the specific positions are:
|
nB/A(t*) = sin30°I - cos30°(K) and tB/A(t*) = cos30°I + sin30°(K) | (4) Values of the unit vectors at this specific time, t = "t*. | e0B = cos15°I - sin15°(K) | (5)
The constant direction of vector 0B. |
Enter this information into Eqn-3.
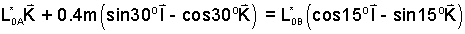
| (6) |
Explicit form of the Position Vector at t = "t*.
Separate Eqn-6 into its components.
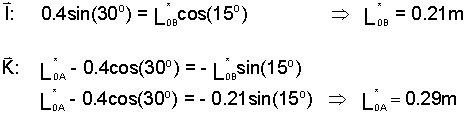
| (7) |
Components of the specific position equation.
These are the "position" results for the specific time.
------------------------------------
Velocity Triangle The derivative of a Position Equation yields its Velocity Equation. The derivative of Eqn-13 is:
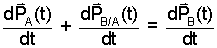
| (8) |
The Velocity Triangle.
From the schematic we can develop the first term and last term in general.
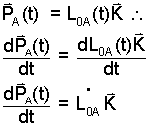
| (9) Position, PA is made explicit. |
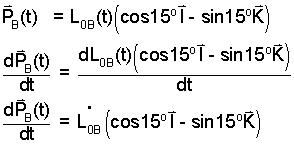
| (10) Position, PB is made explicit. |
Write these partial results in replacement of the left-most and right-most terms of Eqn-8.
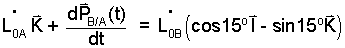
| (11) |
The derivative, dPBA/dt, requires special consideration.
The remaining differentiation (2nd term) addresses Bar-AB. For this differentiation we must use the normal/tangent pair of unit vectors attached to Bar-AB: nB/A(t), and tB/A(t).
Eqn-3 shows PBA(t). The derivative of a rotating unit vector equals a second unit vector, perpendicular to the first, and directed in the direction of increasing angle times the angular rate. Thus:
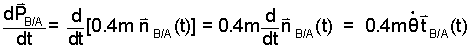
| (12) |
Read More the derivative of a unit vector.
Rewrite Eqn-11 and insert the result (Eqn-12; right-most-form) to obtain:
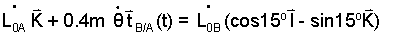
| (13) |
Explicit Form of the Velocity Triangle.
Eqn-13 is our Velocity Triangle, its motion being a function of time.
Velocity Specialization at t = t*: Of immediate concern are the velocity magnitudes at t = t*. For t = t*, the unit tangent is tB/A(t*) = cos30°I + sin30°K. Also by the problem statement we have L0B - dot * = 0.5 m/s.
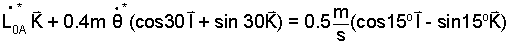
| (14) |
At t = t*.
Break into components:
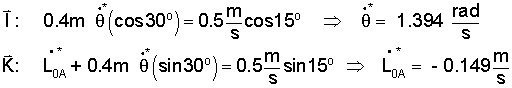
| (15) |
Component of Velocity Triangle at t = t*
------------------------------------
Acceleration Triangle: The derivative of a Velocity Equation, Eqn-13, yields an Acceleration Equation.
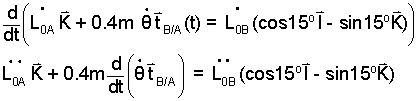
| (16) |
e016
The next equation displays the differentiation of the second term.
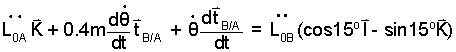
| (17) |
e017
Mechanisms are tedious but straight-forward. Some educators teach "tricks" whereby some special number is "pulled from a hat." For design of a "to function" mechanism, single solutions are not enough. Knowledge of all positions, speeds, etc. are needed. A general, though tedious (as I said) approach is best. There is no other path to computer simulation of the mechanism. I'm leaving this here to continue later - upon show of interest of someone. Want to see more? Contact me at THERMO Spoken Here!
Kinematics of Bar-AB
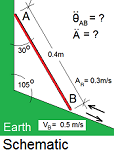
Typical text-book "given-information" sketch.
"Bar-AB and Ground" constitute a kinematic mechanism. Connections at A and B (not shown) maintain sliding contact with the ground. At the instant shown, End-B has a velocity of 0.5m/s and an acceleration of 0.3m/s² (in the directions shown). Calculate the angular acceleration of the Bar-AB and the acceleration of End-A.
Premise presently unwritted!