| THERMO Spoken Here! ~ J. Pohl © ( A4380~3/15) | ( A4400 - 1.19 Dummy Variable) |
1.18 Value, Slope and Curvature
Analytic Geometry has provided capable tools for description of a BODY in motion in space. To describe physical space (called 3-space by some) requires specification of three dimensions. A fourth dimension, time, is needed when events being both spacially and temporally dependent.
Steps required to prescribe a coordinate space include:
(i) Selection an "origin" (some say "a point in space") must be made. Within the space of the event (observed or imagined), a point must be chosen (in the yet undefined space) to be the "origin" or center location. An "origin" (fortuitously chosen) can be a convenience in understanding regarding the BODY/event future.
(ii) At the chosen origin, three mutually-perpendicular straight lines are imagined to extend. These lines, called "coordinates" are (by convention) named X, (or the "X-coordinate"), Y, and Z. These upper-case letters, their orientations, denote, each their respective coordinate. Coordinates are lines. In addition, (by convention here) the axes are numerated using as notation, the lower cast letters, "x", "y" and "z".
To be clear: A BODY located at the origin has numerated position: 0,0,0. Meaning the numerated values of coordinates are (lower-case letters): x = 0, y = 0, and z = 0
(iii) In our beginning-level usages, only two of the three axes are used. At our learner's level only two dimensions, only planar considereations, are needed. The cartesian coordinates, X and Y, (designating a horizontal plane) are chosen for motion of any BODY being independent of gravity. X and t are the coordinates of linear motion of a BODY in time. Should gravity force be relevant, coordinates Z and t would be used (our convention is Earth reference, with "z positive upward."
Value, Slope and Curvature are the information about a Curve at
a point on the curve
More Later - This work is in progress."
Methods of physics and math (about reality simplified to be a BODY) can predict future aspects of a BODY/events quantitatively. The "things," for a BODY (or any other model of physical reality) are its properties and its characteristics. Features of matter itself, that change are called properties. The BODY has one property which is constant - its mass. The vector quantities, position, velocity and acceleration are called characteristics.
Consider a hypothetical property notated as, F, which changes only as does time. That property is written symbolically as: F(t). For us, any observation of some F(t) over time must begin at (the beginning of its
observation) x = x*:
A basic idea of calculus is that a function, F(t), has three characteristics at any specified value of t, say x = x*. Associated with x* the function has a a value, a slope and curvature. These ideas are illustrated in the sketches below.
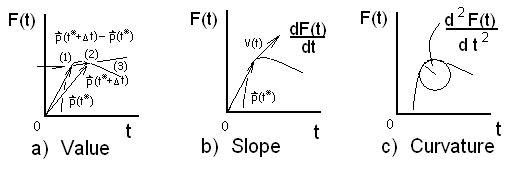
1.18 Value, Slope and Curvature
Science uses mathematics to describe events of physical reality in time. Here is discussed "function of time." Newton viewed reality and its mathematical description to be the same in the limit of very change, short instances in time. At an instance, say at t = t*, physical reality described by a mathematical function has a value, a change of that value (function slope) and a curvature. Value, slope and curvature, that mathematics, explains, physical behaviors at their basis.
Premise presently unwritted!